Mathematics
In the figure (i) given below, two circles with centers C, D intersect in points P, Q. If length of common chord is 6 cm and CP = 5 cm, DP = 4 cm, calculate the distance CD correct to two decimal places.
Circles
10 Likes
Answer
From figure,
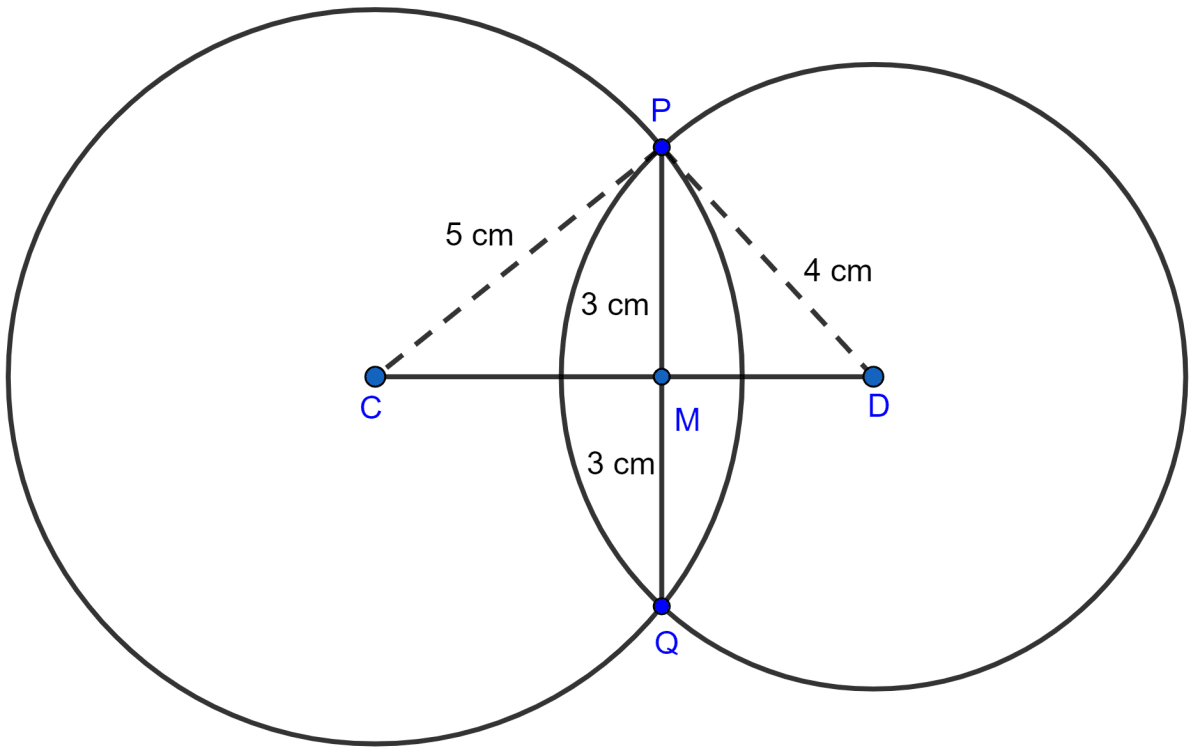
PM = MQ = = 3 cm.
In right △CMP,
⇒ CP2 = CM2 + PM2 (By pythagoras theorem)
⇒ 52 = CM2 + 32
⇒ CM2 = 25 - 9
⇒ CM2 = 16
⇒ CM = = 4 cm.
In right △DMP,
⇒ DP2 = DM2 + PM2 (By pythagoras theorem)
⇒ 42 = DM2 + 32
⇒ DM2 = 16 - 9
⇒ DM2 = 7
⇒ DM = = 2.65 cm.
CD = CM + MD = 4 + 2.65 = 6.65 cm.
Hence, CD = 6.65 cm.
Answered By
4 Likes
Related Questions
The radii of two concentric circles are 17 cm and 10 cm; a line PQRS cuts the larger circle at P and S and the smaller circle at Q and R. If QR = 12 cm, calculate PQ.
A chord of length 48 cm is at a distance of 10 cm from the centre of a circle. If another chord of length 20 cm is drawn in the same circle, find its distance from the center of the circle.
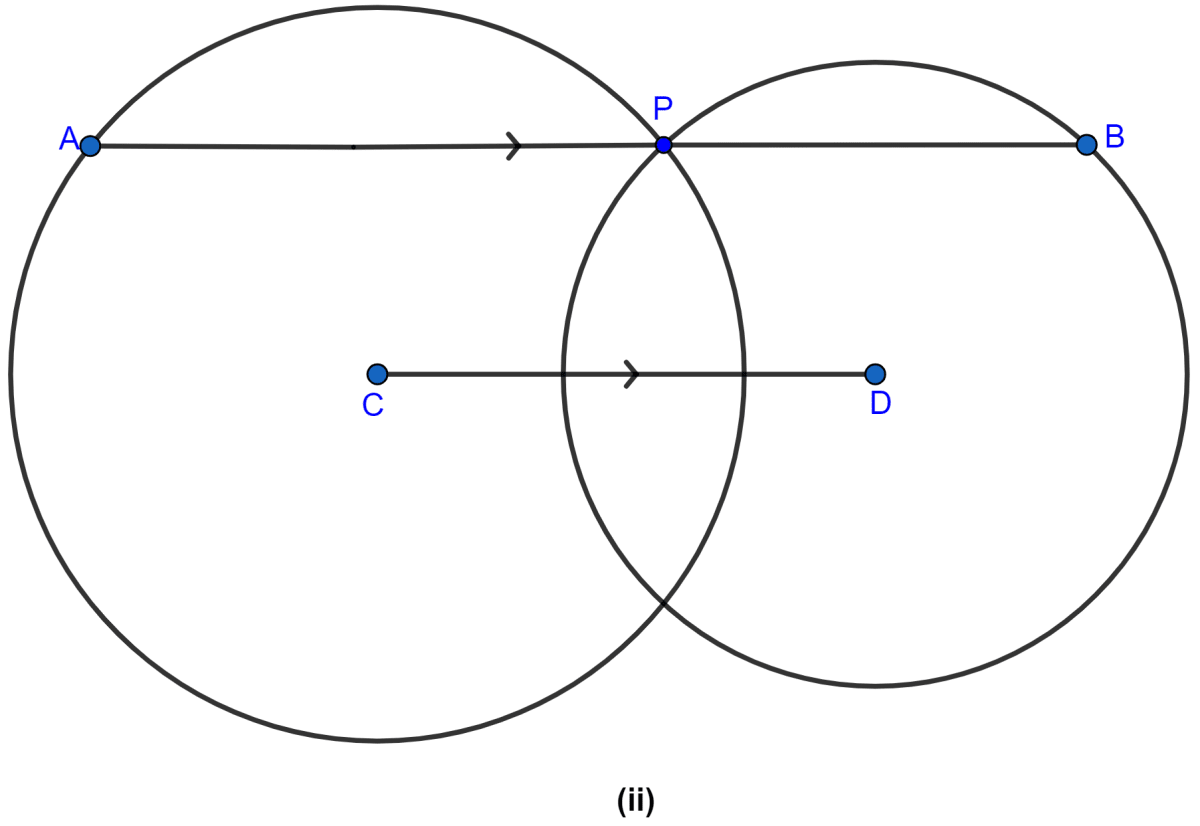
In the figure (ii) given below, P is a point of intersection of two circles with centers C and D. If the st. line APB is parallel to CD, prove that AB = 2CD.
In the figure (i) given below, C and D are centers of two intersecting circles. The line APQB is perpendicular to the line of centers CD. Prove that
(i) AP = QB
(ii) AQ = BP.
