Mathematics
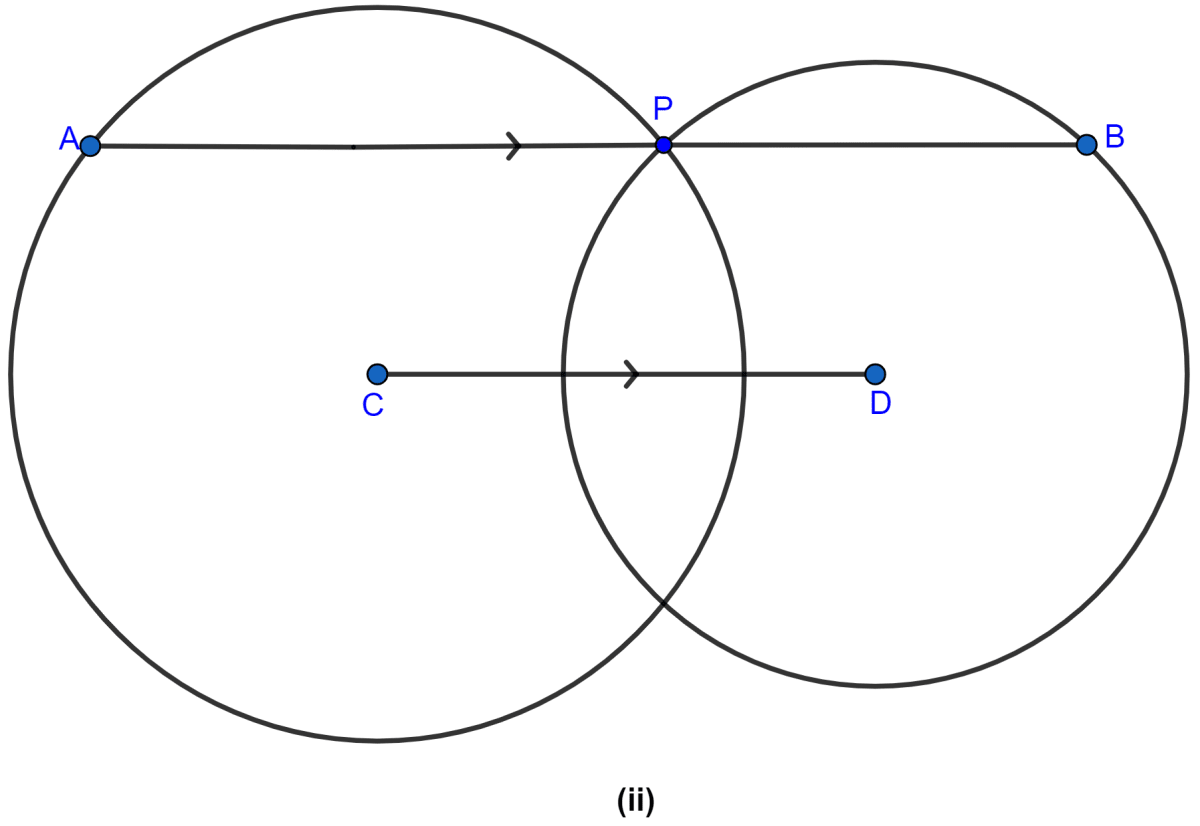
In the figure (ii) given below, P is a point of intersection of two circles with centers C and D. If the st. line APB is parallel to CD, prove that AB = 2CD.
Circles
32 Likes
Answer
From C, D draw CM, DN perpendiculars to AB.
From figure,
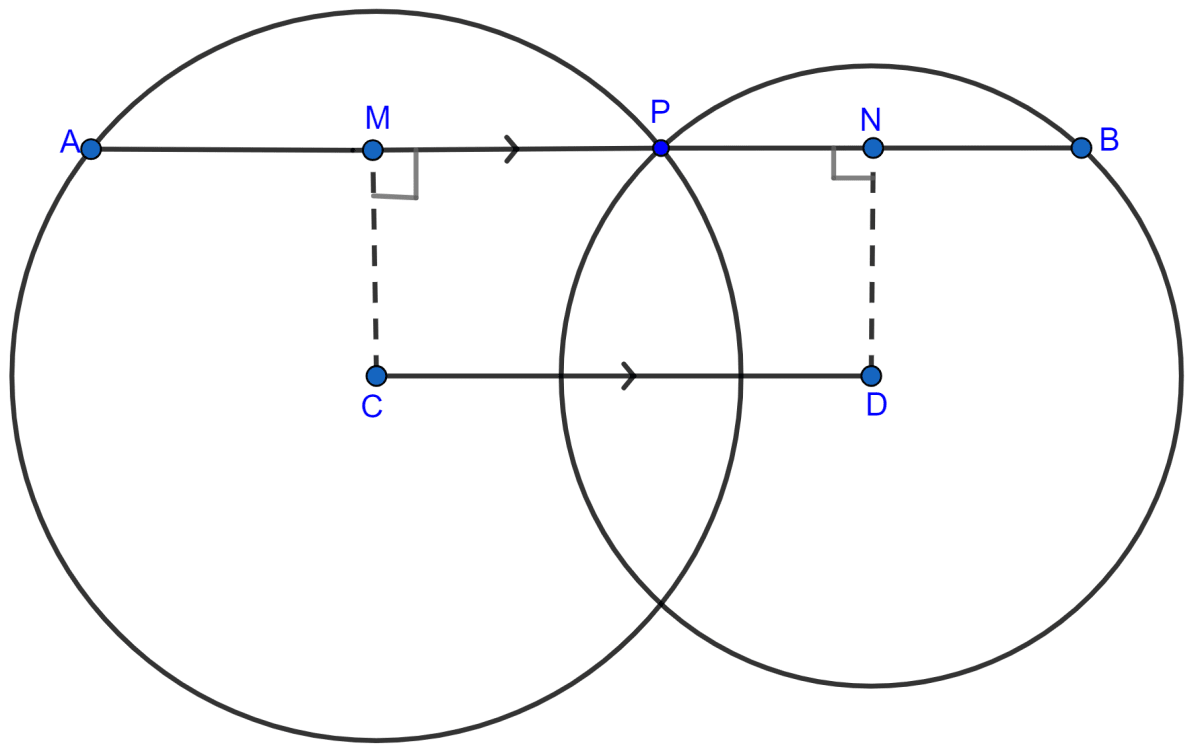
MCDN is a rectangle.
∴ MN = CD (Opposite sides of rectangle are equal).
Since, the perpendicular to a chord from the centre of the circle bisects the chord,
∴ MP = AP and NP = PB
From figure,
MN = MP + PN
= AP + PB
= (AP + PB)
= AB
∴ CD = AB [∵ MN = CD]
⇒ AB = 2CD
Hence, proved that AB = 2CD.
Answered By
19 Likes
Related Questions
A chord of length 48 cm is at a distance of 10 cm from the centre of a circle. If another chord of length 20 cm is drawn in the same circle, find its distance from the center of the circle.
In the figure (i) given below, two circles with centers C, D intersect in points P, Q. If length of common chord is 6 cm and CP = 5 cm, DP = 4 cm, calculate the distance CD correct to two decimal places.
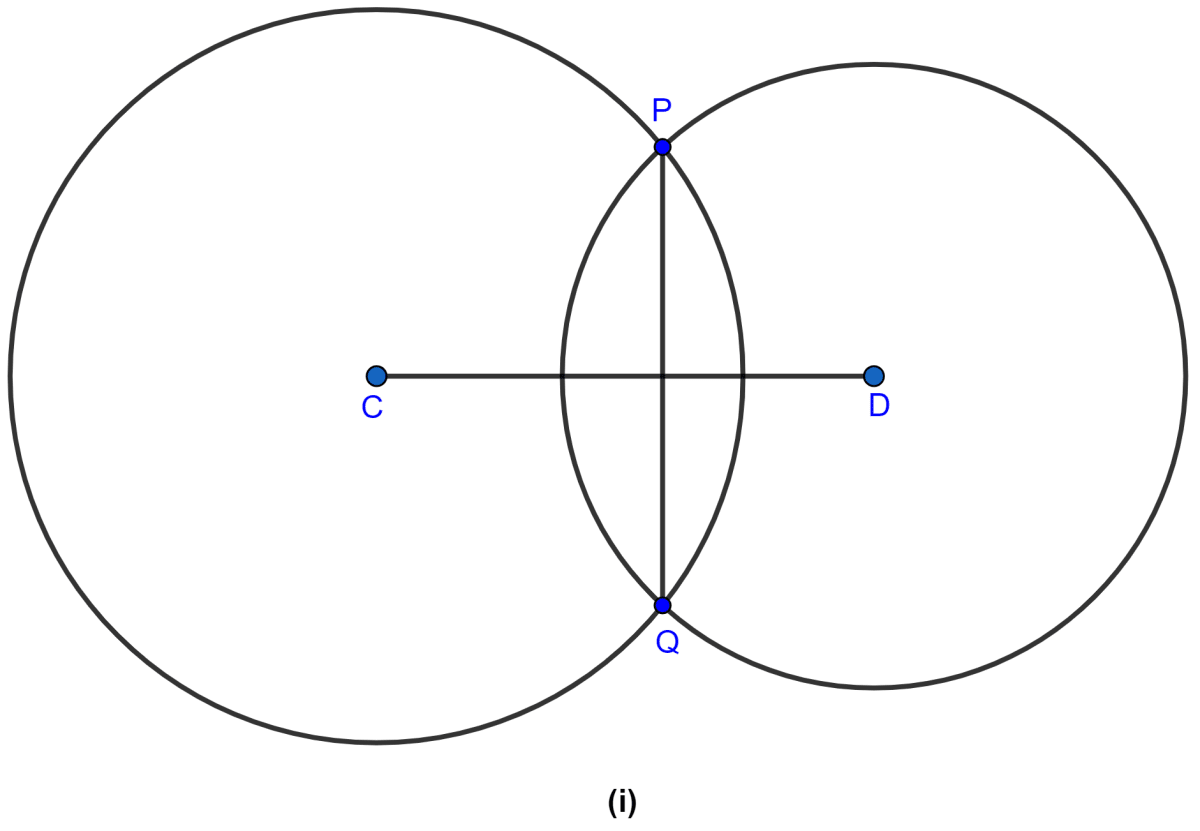
In the figure (i) given below, C and D are centers of two intersecting circles. The line APQB is perpendicular to the line of centers CD. Prove that
(i) AP = QB
(ii) AQ = BP.

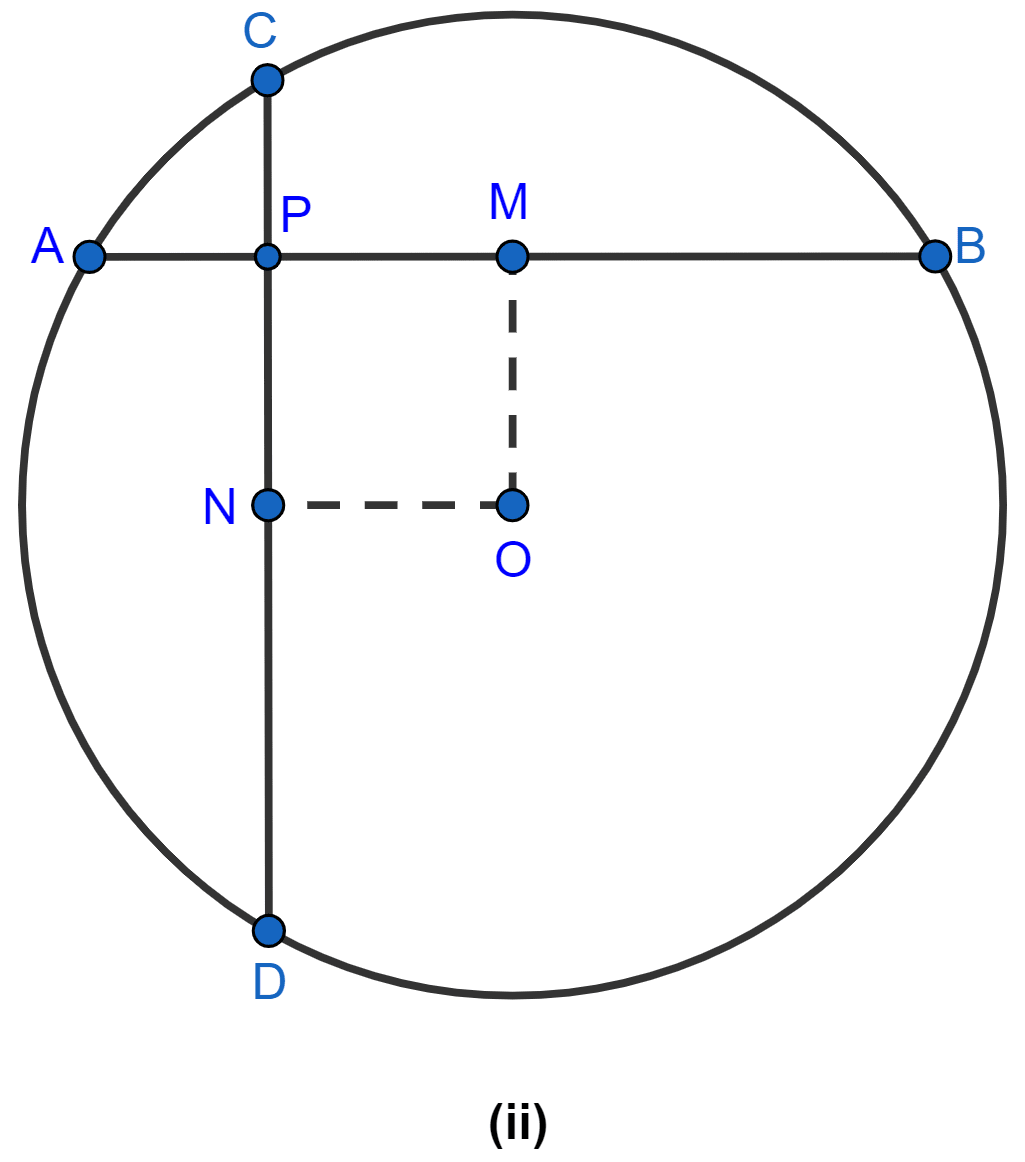
In the figure (ii) given below, two equal chords AB and CD of a circle with center O intersect at right angles at P. If M and N are mid-points of the chords AB and CD respectively, prove that NOMP is a square.