Mathematics
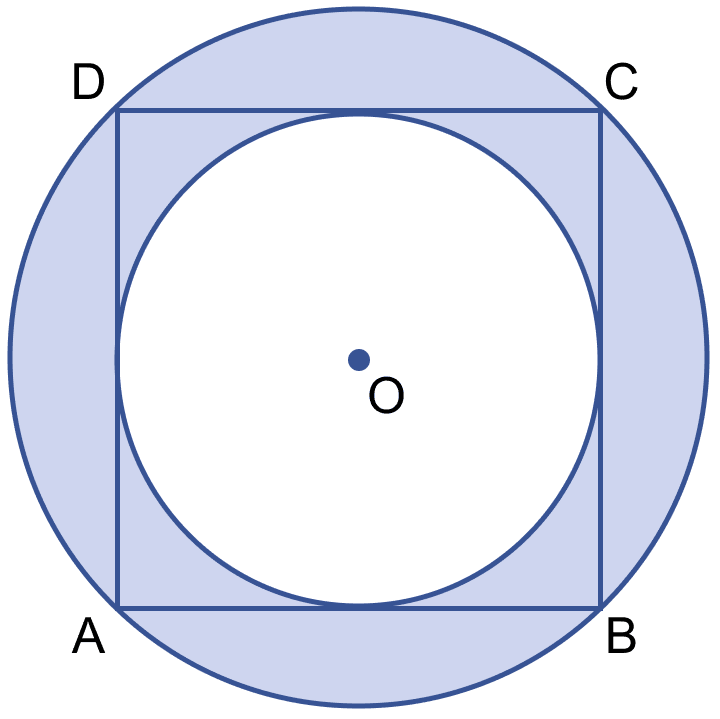
In the adjoining figure, ABCD is a square. Find the ratio between
(i) the circumferences
(ii) the areas of the incircle and the circumcircle of the square.
Mensuration
37 Likes
Answer
(i) Let side of the square be 2a units.
From figure,
AD = Diameter of incircle.
Radius of incircle (r) = = a units.
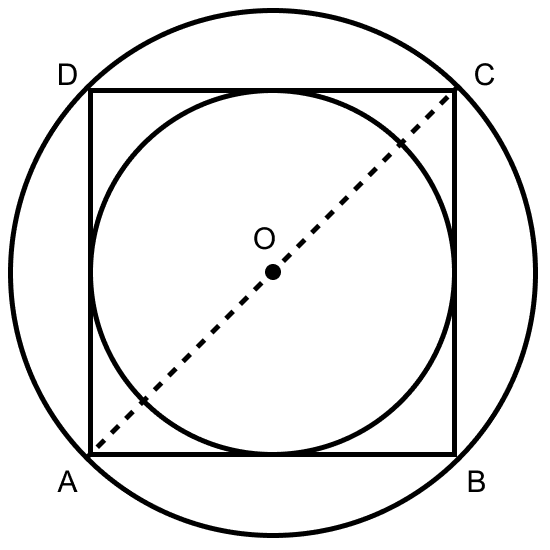
In right angle triangle ABC,
Using pythagoras theorem,
AC2 = AB2 + BC2
AC2 = (2a)2 + (2a)2
AC2 = 4a2 + 4a2
AC2 = 8a2
AC = units.
From figure,
AC is the diameter of circumcircle and AO is radius.
AO (R) = a units.
Hence, ratio between circumferences = .
(ii)
Hence, ratio between areas = 1 : 2.
Answered By
25 Likes
Related Questions
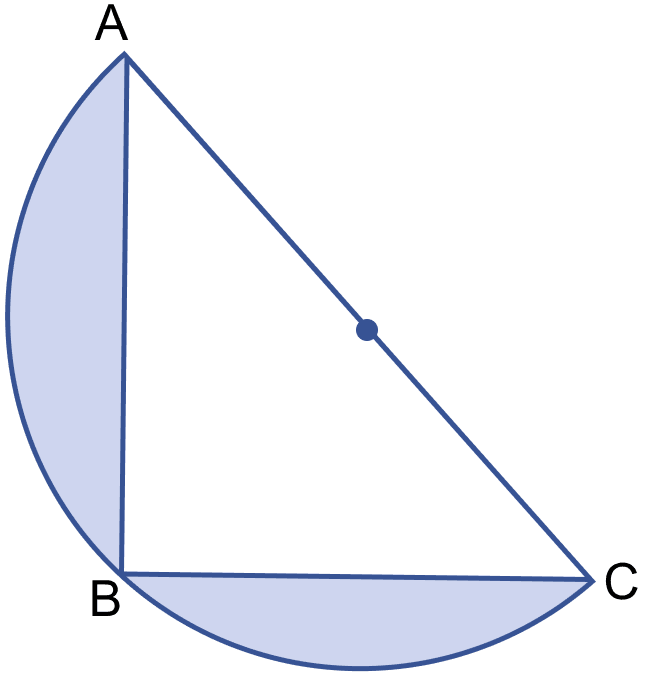
In the figure (ii) given below, ABC is an isosceles right angled triangle with ∠ABC = 90°. A semicircle is drawn with AC as diameter. If AB = BC = 7 cm, find the area of the shaded region. Take π = .
A circular field has perimeter 660 m. A plot in the shape of a square having its vertices on the circumference is marked in the field. Calculate the area of the square field.
The figure (i) given below shows a running track surrounding a grassed enclosure PQRSTU. The enclosure consists of a rectangle PQST with a semicircular region at each end. PQ = 200 m; PT = 70 m.
(i) Calculate the area of the grassed enclosure in m2.
(ii) Given that the track is of constant width 7 m, calculate the outer perimeter ABCDEF of the track.
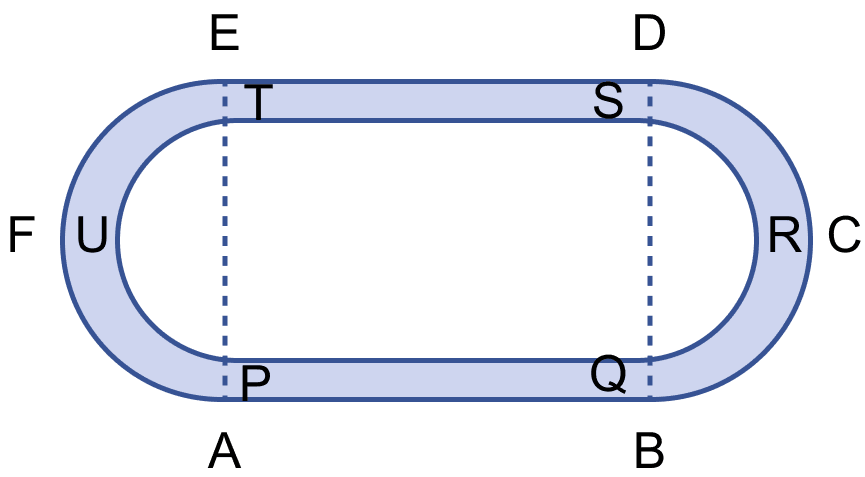
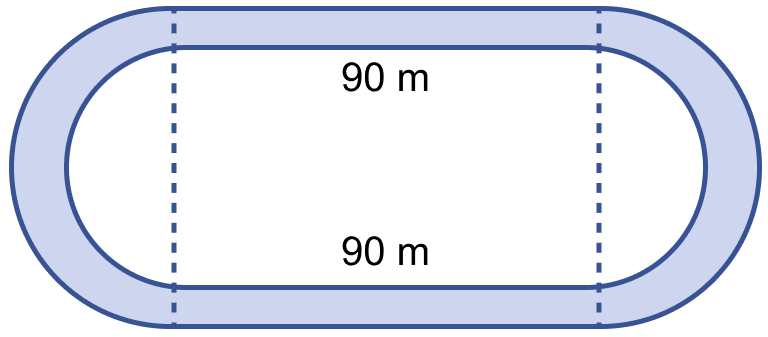
In the figure (ii) given below, the inside perimeter of a practice running track with semi-circular ends and straight parallel sides is 312 m. The length of the straight portion of the track is 90 m. If the track has a uniform width of 2 m throughout, find its area.