Mathematics
A circular field has perimeter 660 m. A plot in the shape of a square having its vertices on the circumference is marked in the field. Calculate the area of the square field.
Mensuration
26 Likes
Answer
By formula,
Perimeter = 2πr
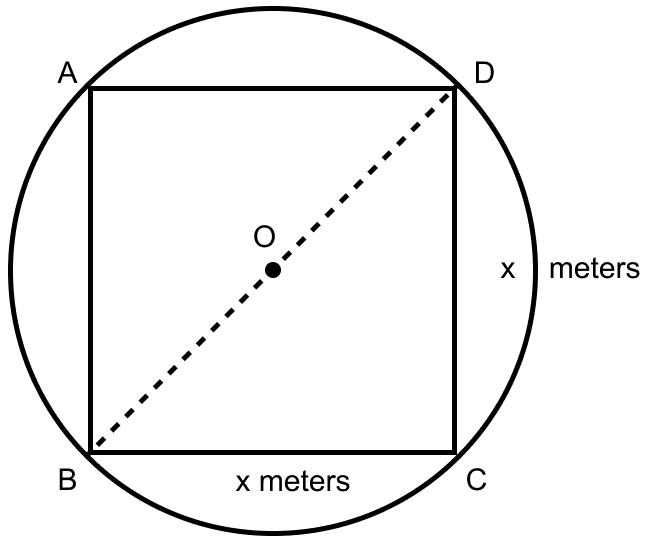
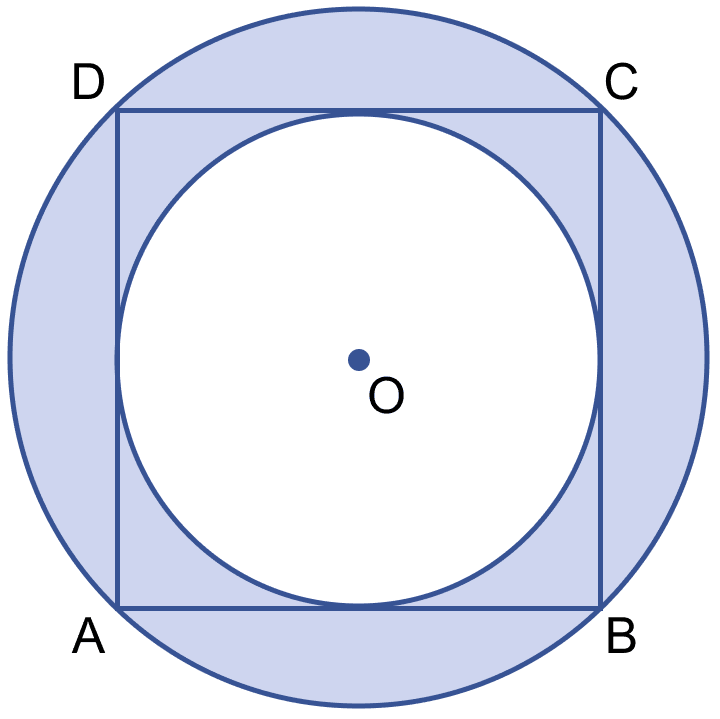
From figure,
BD = BO + OD = r + r = 2r = 2 × 105 = 210 m.
Let O be the center of the circle and ABCD be square of side x metres.
Area of square = (side)2 = x2.
In right angle triangle BCD,
⇒ BD2 = BC2 + CD2
⇒ 2102 = x2 + x2
⇒ 2x2 = 44100
⇒ x2 = = 22050 m2.
Hence, area of square = 22050 m2.
Answered By
16 Likes
Related Questions
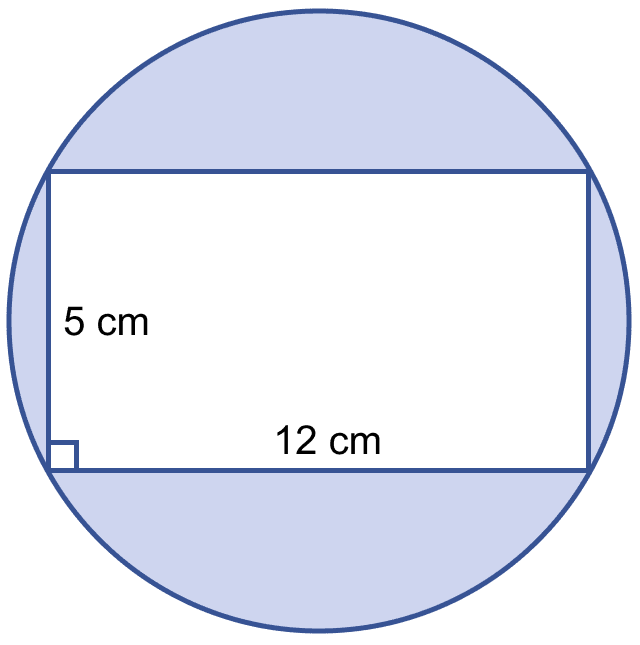
In the figure (i) given below, calculate the area of the shaded region correct to two decimal places. (Take π = 3.142)
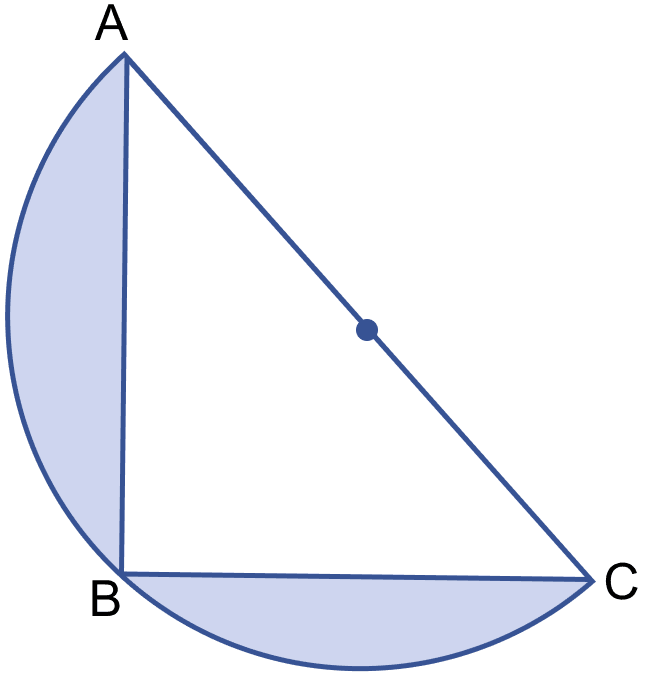
In the figure (ii) given below, ABC is an isosceles right angled triangle with ∠ABC = 90°. A semicircle is drawn with AC as diameter. If AB = BC = 7 cm, find the area of the shaded region. Take π = .
In the adjoining figure, ABCD is a square. Find the ratio between
(i) the circumferences
(ii) the areas of the incircle and the circumcircle of the square.
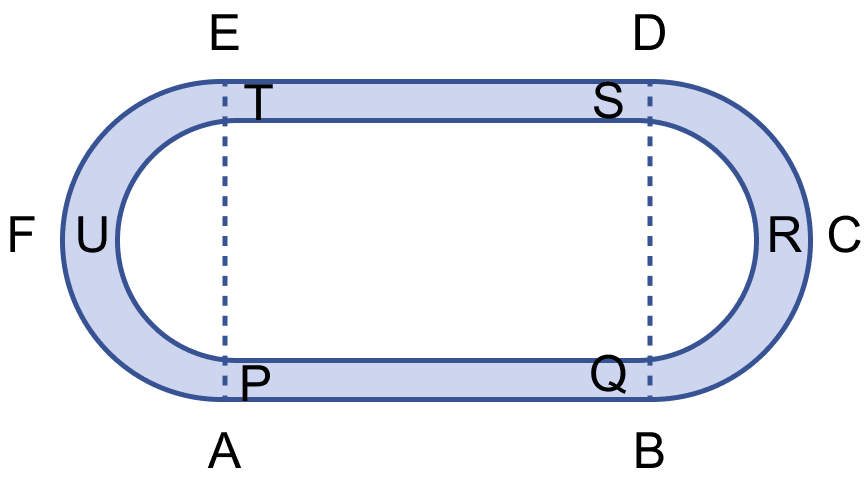
The figure (i) given below shows a running track surrounding a grassed enclosure PQRSTU. The enclosure consists of a rectangle PQST with a semicircular region at each end. PQ = 200 m; PT = 70 m.
(i) Calculate the area of the grassed enclosure in m2.
(ii) Given that the track is of constant width 7 m, calculate the outer perimeter ABCDEF of the track.