Mathematics
In the figure (i) given below, calculate the area of the shaded region correct to two decimal places. (Take π = 3.142)
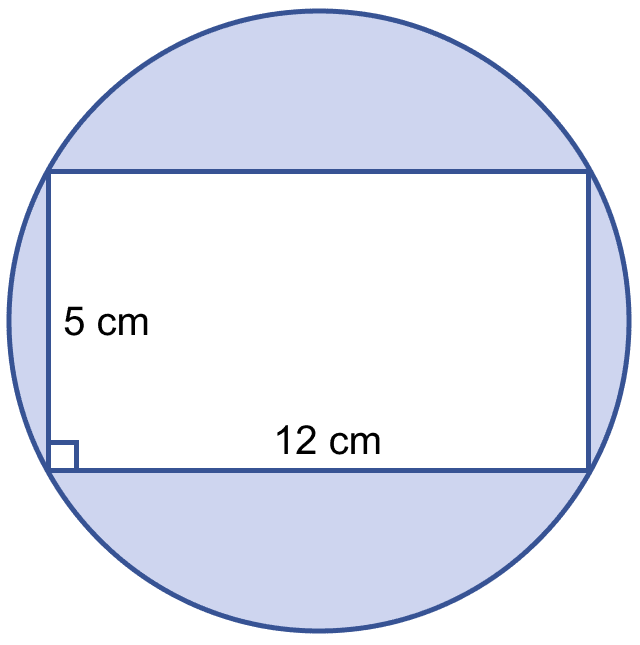
Mensuration
13 Likes
Answer
From figure,
O is the center. In right angle triangle ABC,
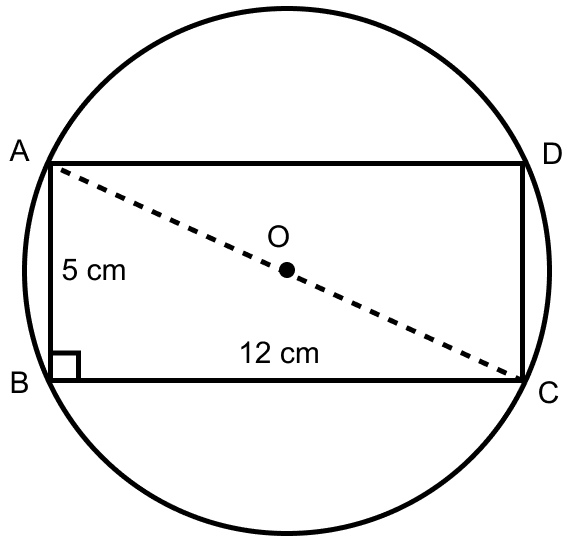
Using pythagoras theorem,
⇒ AC2 = AB2 + BC2
⇒ AC2 = 52 + 122
⇒ AC2 = 25 + 144 = 169
⇒ AC = = 13 cm.
From figure,
AC is the diameter and OA is the radius = = 6.5 cm.
Area of circle = πr2
= 3.142 × (6.5)2
= 3.142 × 42.25
= 132.75 cm2.
Area of rectangle = l × b
= 12 × 5 = 60 cm2.
Area of shaded region = Area of circle - Area of rectangle
= 132.75 - 60
= 72.75 cm2.
Hence, area of shaded region = 72.75 cm2.
Answered By
6 Likes
Related Questions
A circular field has perimeter 660 m. A plot in the shape of a square having its vertices on the circumference is marked in the field. Calculate the area of the square field.
A student takes a rectangular piece of paper 30 cm long and 21 cm wide. Find the area of the biggest circle that can be cut out from the paper. Also find the area of the paper left after cutting out the circle.
A rectangle with one side 4 cm is inscribed in a circle of radius 2.5 cm. Find the area of the rectangle.
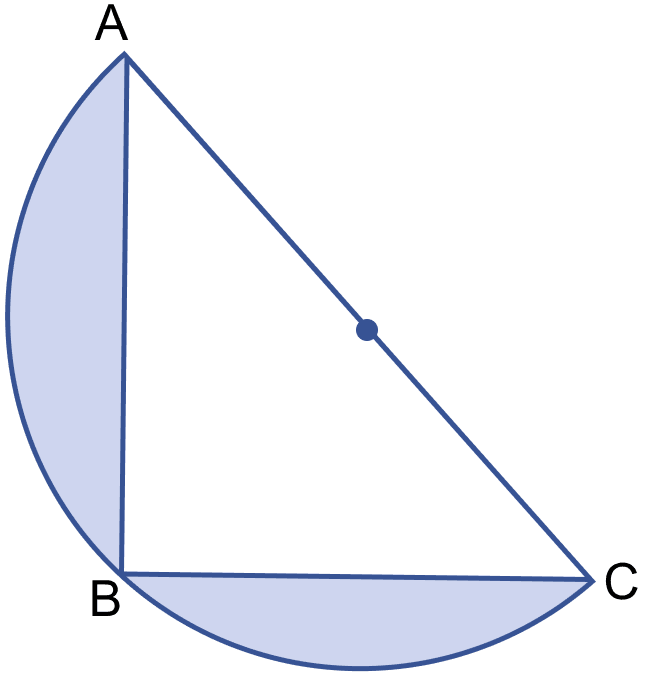
In the figure (ii) given below, ABC is an isosceles right angled triangle with ∠ABC = 90°. A semicircle is drawn with AC as diameter. If AB = BC = 7 cm, find the area of the shaded region. Take π = .
