Mathematics
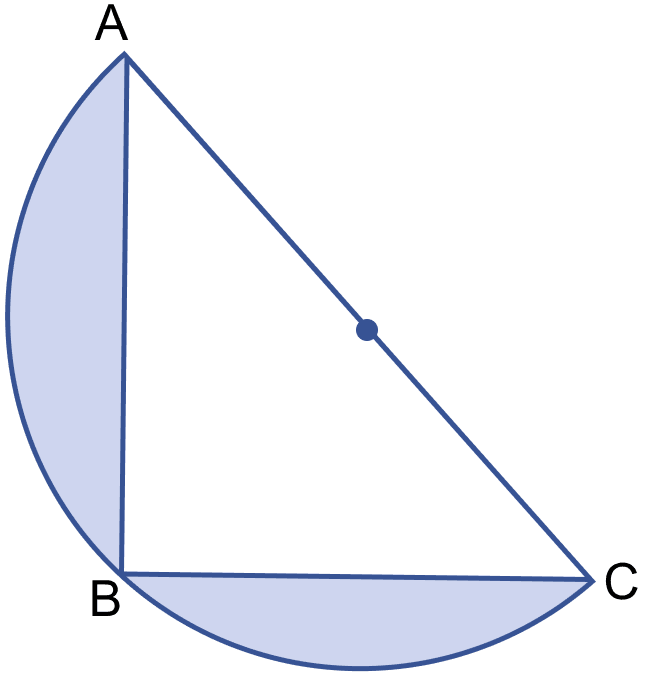
In the figure (ii) given below, ABC is an isosceles right angled triangle with ∠ABC = 90°. A semicircle is drawn with AC as diameter. If AB = BC = 7 cm, find the area of the shaded region. Take π = .
Mensuration
36 Likes
Answer
By formula,
Area of △ABC = × base × height
= × BC × AB
= × 7 × 7
= = 24.5 cm2.
In right angle triangle,
Using pythagoras theorem,
⇒ AC2 = AB2 + BC2
⇒ AC2 = 72 + 72
⇒ AC2 = 49 + 49 = 98
⇒ AC = cm.
From figure,
Radius of semi-circle (r) =
By formula,
Area of semi-circle =
Area of the shaded region = Area of the semi-circle – Area of △ABC
= 38.5 - 24.5
= 14 cm2.
Hence, area of the shaded region = 14 cm2.
Answered By
19 Likes
Related Questions
A rectangle with one side 4 cm is inscribed in a circle of radius 2.5 cm. Find the area of the rectangle.
In the figure (i) given below, calculate the area of the shaded region correct to two decimal places. (Take π = 3.142)
A circular field has perimeter 660 m. A plot in the shape of a square having its vertices on the circumference is marked in the field. Calculate the area of the square field.
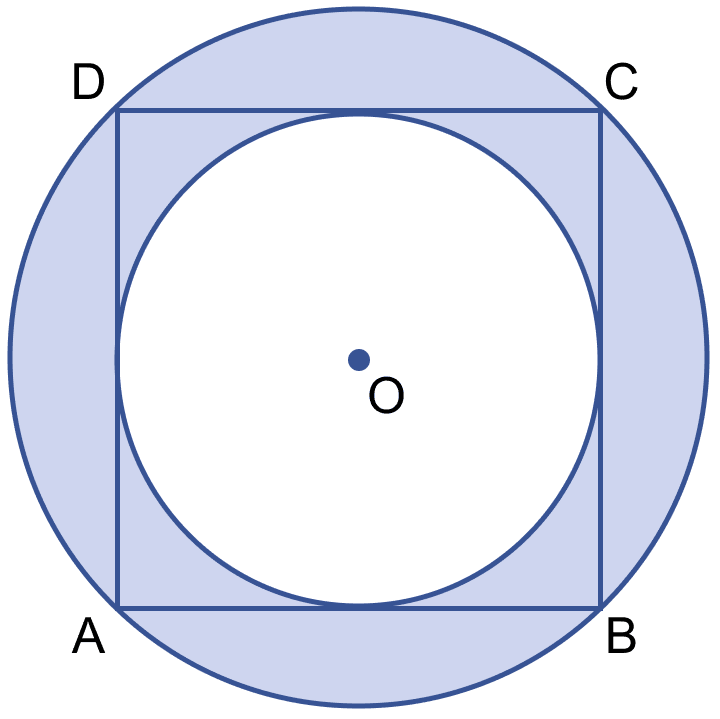
In the adjoining figure, ABCD is a square. Find the ratio between
(i) the circumferences
(ii) the areas of the incircle and the circumcircle of the square.