Mathematics
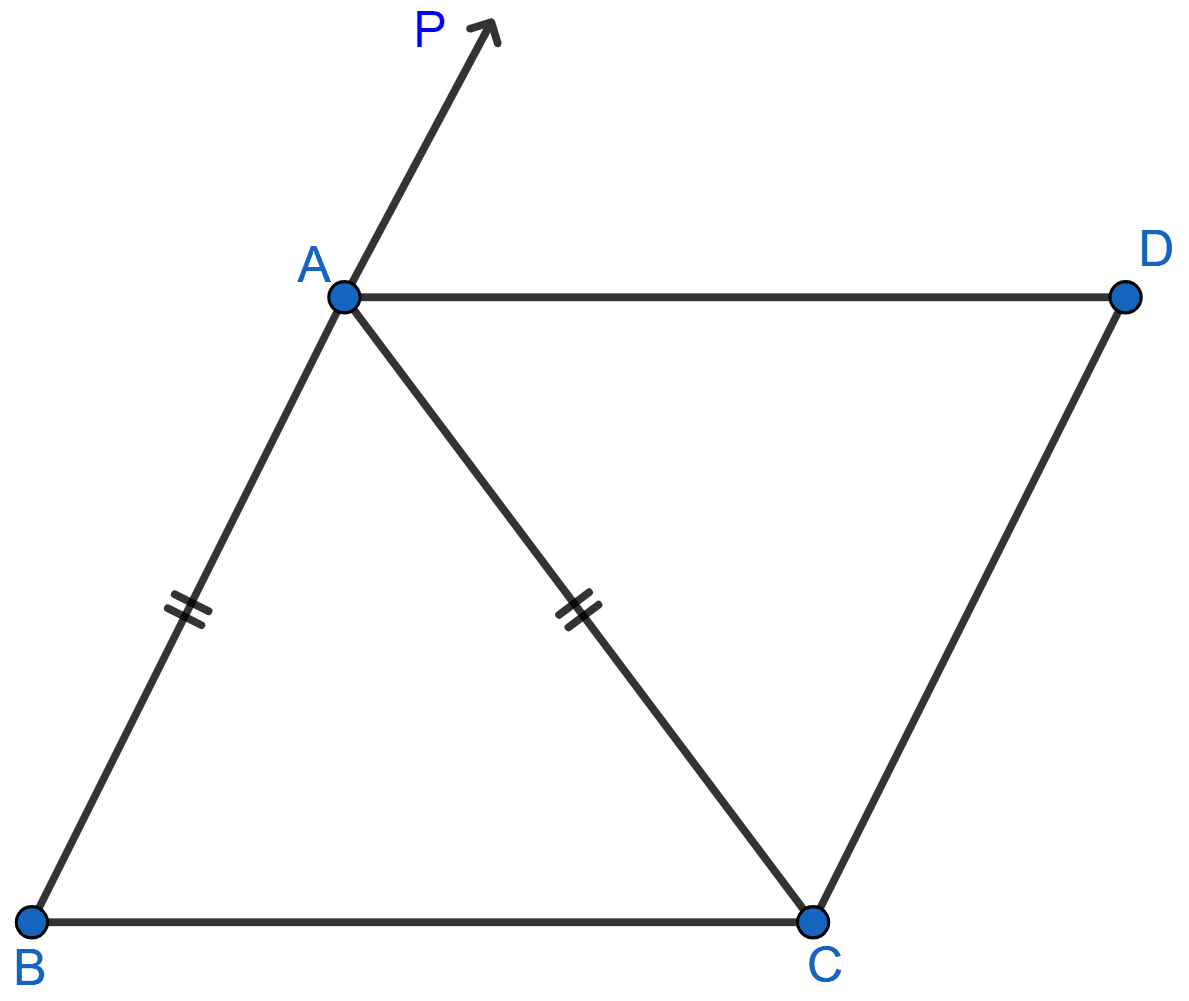
In the adjoining figure, ABC is an isosceles triangle in which AB = AC. AD bisects exterior angle PAC and CD || BA. Show that
(i) ∠DAC = ∠BCA
(ii) ABCD is a parallelogram.
Answer
(i) In ∆ABC
AB = AC [Given]
∠C = ∠B [Angles opposite to equal sides are equal]
Since, ext. ∠PAC = ∠B + ∠C (Exterior angle is equal to the sum of opposite interior angles)
= ∠C + ∠C
= 2∠C
= 2∠BCA
Since AD bisects ext. ∠PAC, ∠PAC = 2∠DAC
⇒ 2∠DAC = 2∠BCA
⇒ ∠DAC = ∠BCA
Hence, proved that ∠DAC = ∠BCA.
(ii) Since, ∠DAC and ∠BCA are alternate angles and AC is transversal.
It proves that AD || BC.
Since, AD || BC and CD || BA.
Hence, proved that ABCD is a || gm.
Related Questions
A quadrilateral in which the diagonals are equal and bisect each other at right angles is a
rectangle which is not a square
rhombus which is not a square
kite which is not a square
square
In the adjoining figure, ABCD is a parallelogram. CB is produced to E such that BE = BC. Prove that AEBD is a parallelogram.

Prove that the quadrilateral obtained by joining the mid-points of an isosceles trapezium is a rhombus.
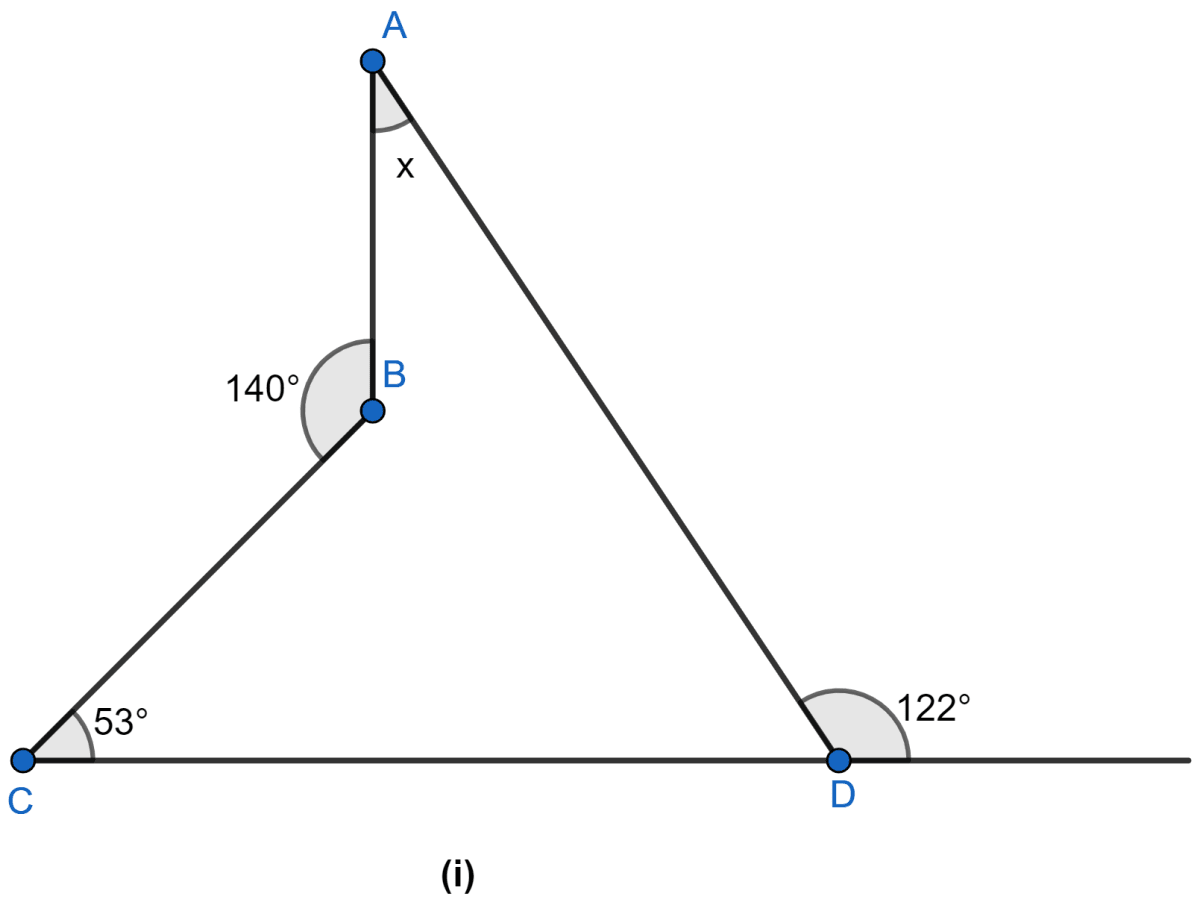
Find the size of each lettered angle in the following figure.