Mathematics
In the adjoining figure, ABCD is a parallelogram. CB is produced to E such that BE = BC. Prove that AEBD is a parallelogram.

Rectilinear Figures
37 Likes
Answer
In ∆AEB and ∆BDC
EB = BC [Given]
∠ABE = ∠DCB [Corresponding angles]
AB = DC [Opposite sides of || gm ABCD are equal]
Thus, ∆AEB ≅ ∆BDC by S.A.S axiom
So, by C.P.C.T
BD = AE
In || gm ABCD,
BC = AD (As opposite sides of || gm are equal)
Given,
BC = BE
∴ AD = BE.
Since, opposite sides of quadrilateral AEBD are equal (i.e., BD = AE and AD = BE)
Hence, proved that AEBD is a parallelogram.
Answered By
20 Likes
Related Questions
Which of the following is not true for a parallelogram?
opposite sides are equal
opposite angles are equal
opposite angles are bisected by the diagonals
diagonals bisect each other
A quadrilateral in which the diagonals are equal and bisect each other at right angles is a
rectangle which is not a square
rhombus which is not a square
kite which is not a square
square
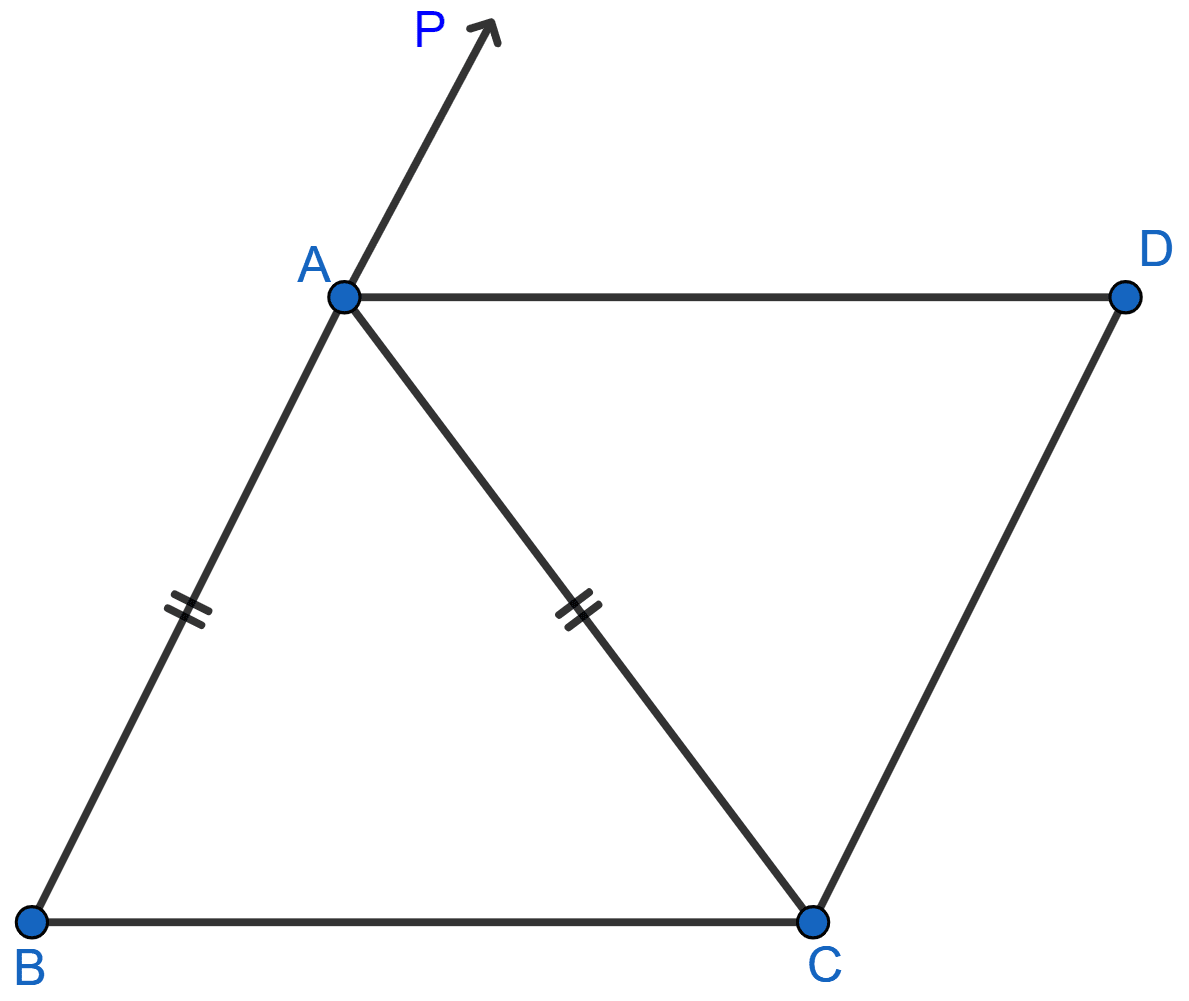
In the adjoining figure, ABC is an isosceles triangle in which AB = AC. AD bisects exterior angle PAC and CD || BA. Show that
(i) ∠DAC = ∠BCA
(ii) ABCD is a parallelogram.
Prove that the quadrilateral obtained by joining the mid-points of an isosceles trapezium is a rhombus.