Mathematics
Prove that the quadrilateral obtained by joining the mid-points of an isosceles trapezium is a rhombus.
Rectilinear Figures
17 Likes
Answer
P, Q, R and S are the mid-points of the sides AB, BC, CD and DA respectively.
Join AC and BD.

Since, ABCD is an isosceles trapezium
Its diagonals are equal.
AC = BD = x (let)
Now, in ∆ABC
P and Q are the mid-points of AB and BC
So, PQ || AC and PQ = AC = x (By midpoint theorem) … (i)
Similarly, in ∆ADC
S and R mid-point of AD and CD
So, SR || AC and SR = AC = x (By midpoint theorem) … (ii)
From (i) and (ii), we have
PQ || SR and PQ = SR = …….(iii)
In ∆CBD,
R and Q are the mid-points of CD and BC
So, QR || BD and QR = BD = x (By midpoint theorem) … (iv)
Similarly, in ∆ABD
S and P mid-point of AD and AB
So, SP || BD and SP = BD = x (By midpoint theorem) … (v)
From (iv) and (v), we have
QR || SP and QR = SP = …….(vi)
From (iii) and (vi) we get,
PQ = QR = SR = SP and QR || SP, PQ || SR.
So, sides of PQRS are equal and opposite sides are parallel.
Hence, proved that PQRS is a rhombus.
Answered By
10 Likes
Related Questions
In the adjoining figure, ABCD is a parallelogram. CB is produced to E such that BE = BC. Prove that AEBD is a parallelogram.

In the adjoining figure, ABC is an isosceles triangle in which AB = AC. AD bisects exterior angle PAC and CD || BA. Show that
(i) ∠DAC = ∠BCA
(ii) ABCD is a parallelogram.
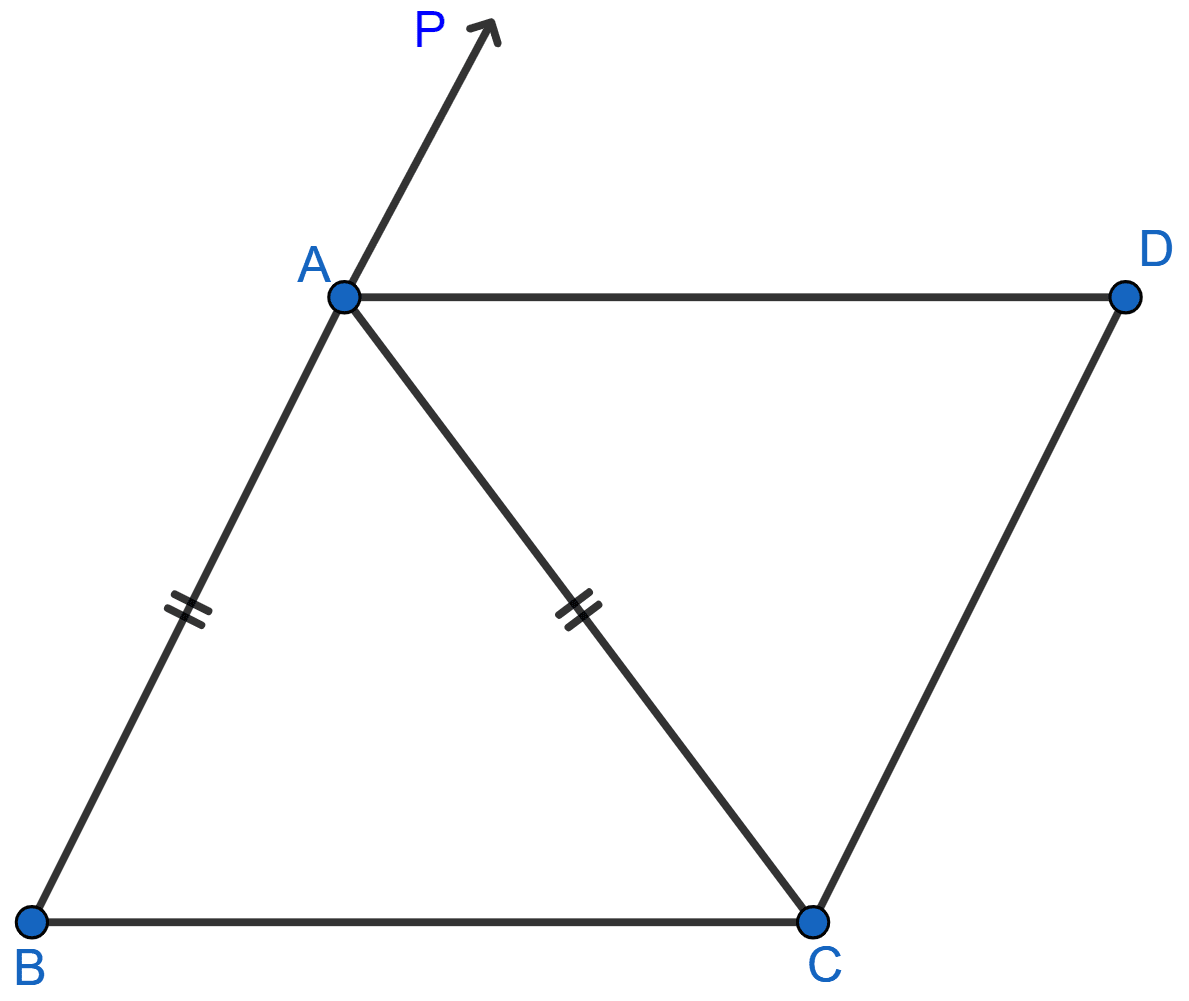
Find the size of each lettered angle in the following figure.
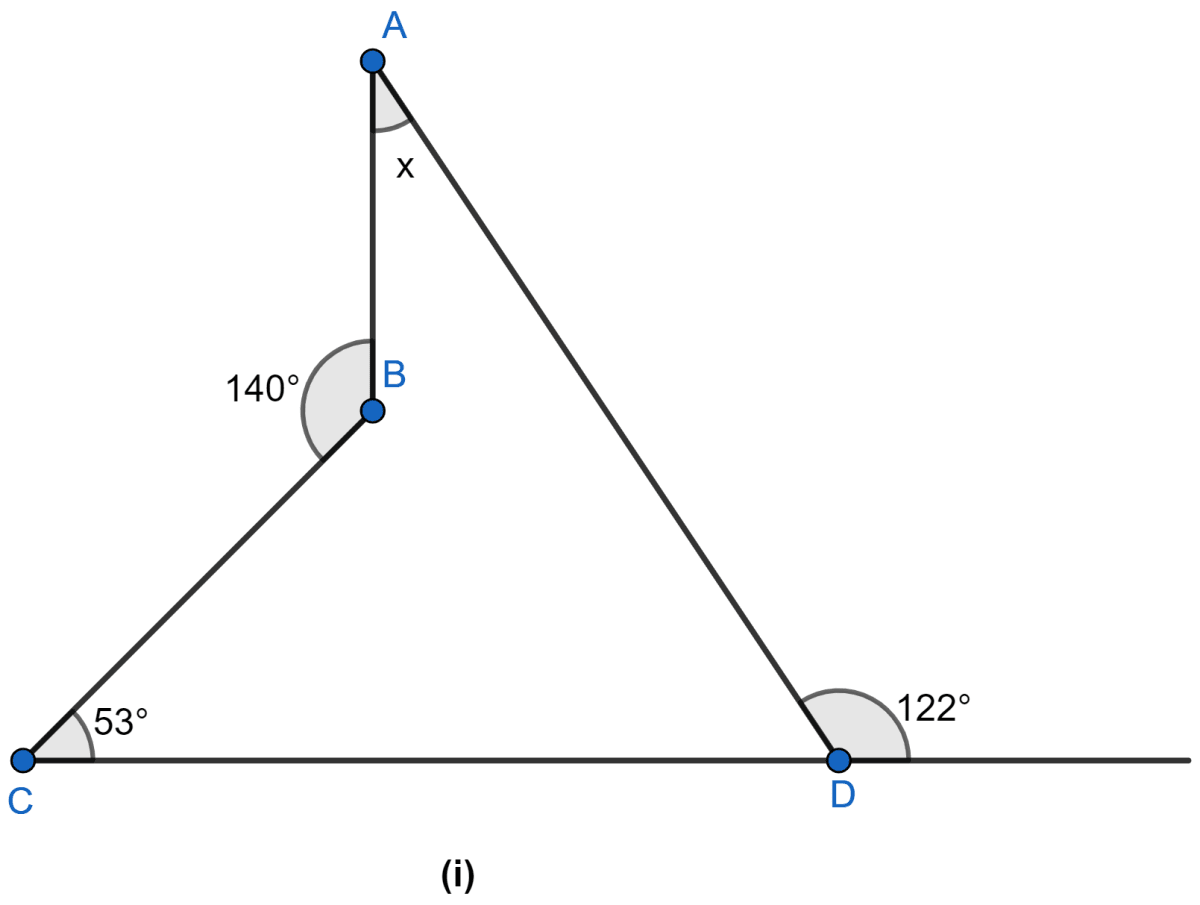
Find the size of each lettered angle in the following figure.
