Mathematics
Find the size of each lettered angle in the following figure.
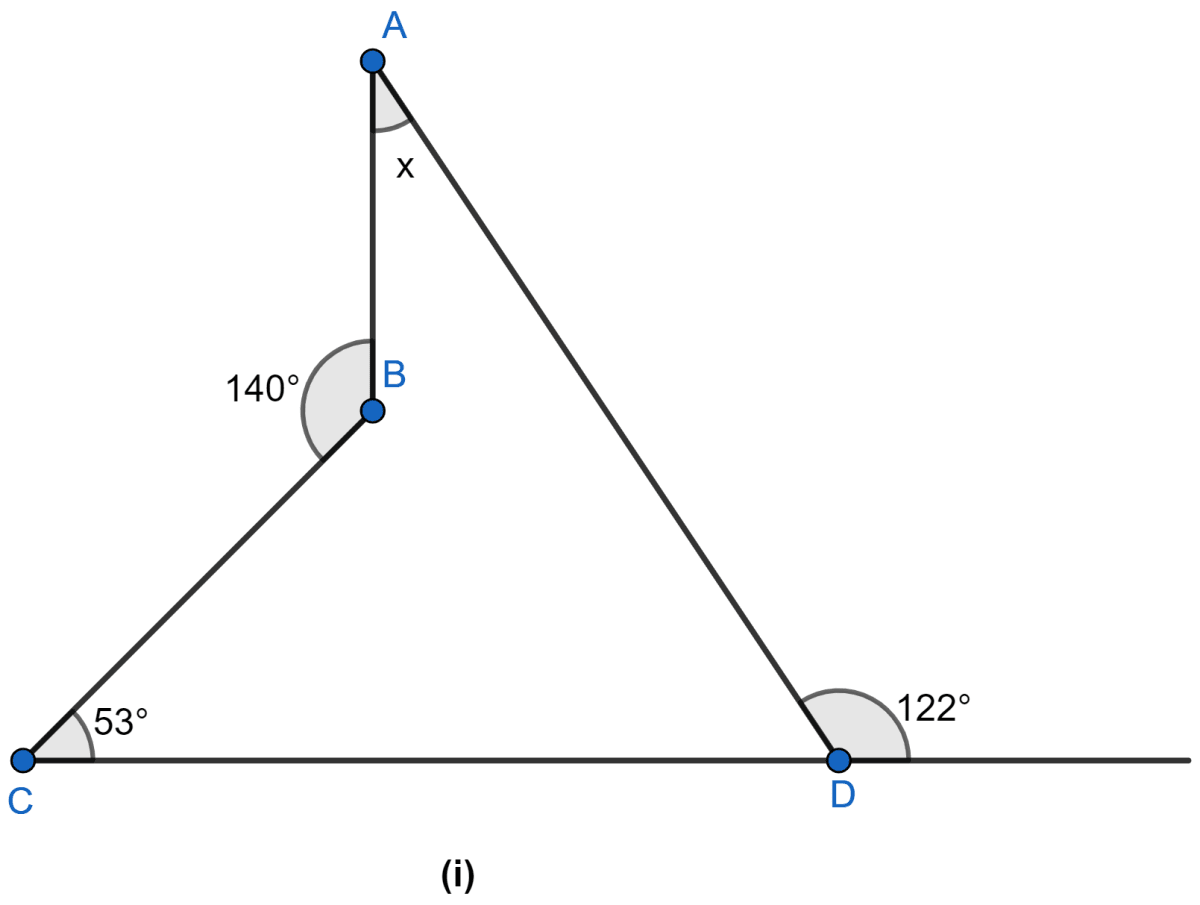
Rectilinear Figures
4 Likes
Answer
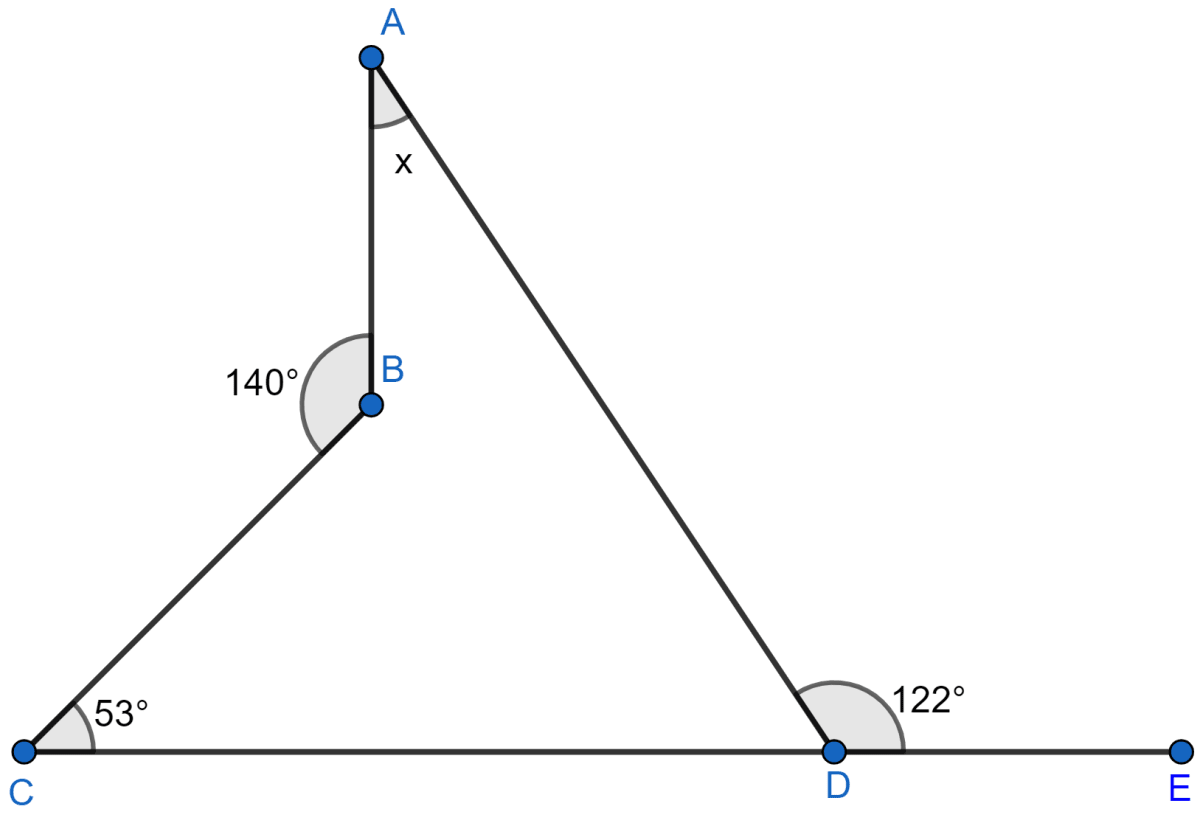
As CDE is a straight line
∠ADE + ∠ADC = 180°
122° + ∠ADC = 180°
∠ADC = 180° – 122° = 58° … (i)
Internal ∠ABC = 360° – 140° = 220° … (ii)
Now, in quadrilateral ABCD we have
⇒ ∠ADC + ∠BCD + ∠BAD + ∠ABC = 360° (As sum of all angles in a quadrilateral is 360°.)
⇒ 58° + 53° + x + 220° = 360° [Using (i) and (ii)]
⇒ 331° + x = 360°
⇒ x = 360° – 331°
⇒ x = 29°
Hence, x = 29°
Answered By
3 Likes
Related Questions
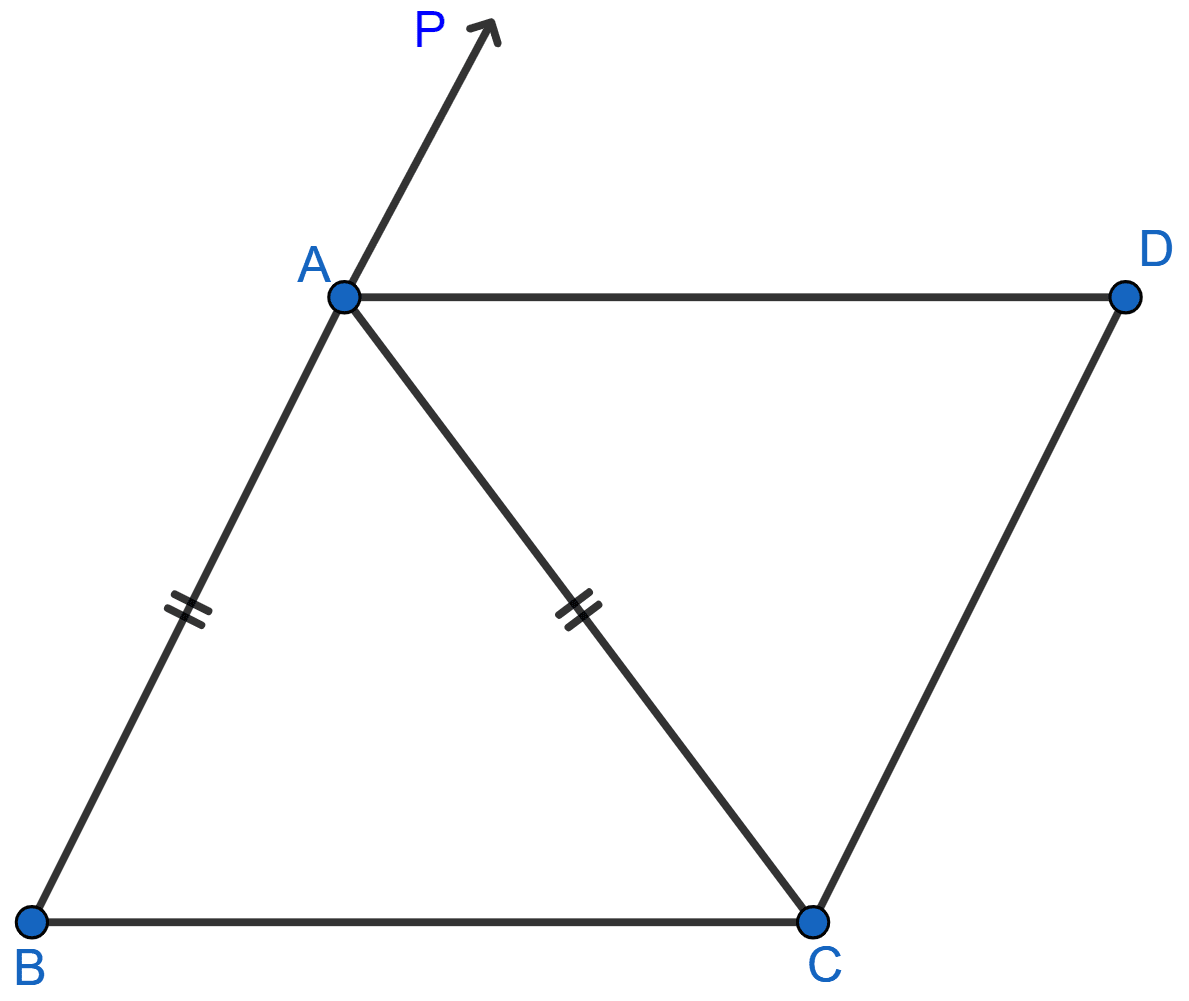
In the adjoining figure, ABC is an isosceles triangle in which AB = AC. AD bisects exterior angle PAC and CD || BA. Show that
(i) ∠DAC = ∠BCA
(ii) ABCD is a parallelogram.
Prove that the quadrilateral obtained by joining the mid-points of an isosceles trapezium is a rhombus.
Find the size of each lettered angle in the following figure.

Find the size of each lettered angle in the following figure.
