Mathematics
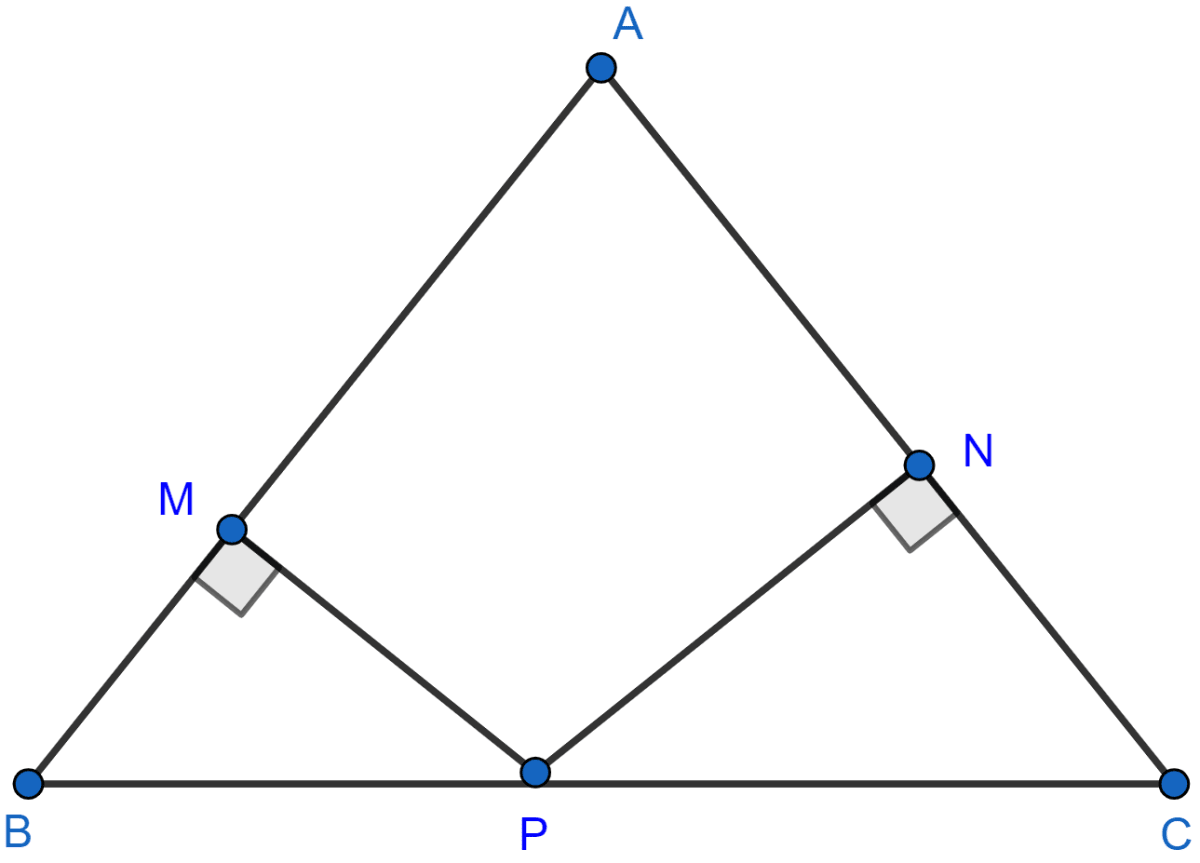
In the adjoining figure, ABC is a triangle in which AB = AC. P is a point on the side BC such that PM ⊥ AB and PN ⊥ AC. Prove that BM × NP = CN × MP.
Similarity
Answer
Consider △ABC
Given, AB = AC
∠ B = ∠ C [Angles opposite to equal sides (Property of isosceles triangle)]
Considering △BMP and △CNP
∠ M = ∠ N = 90°.
∠ B = ∠ C.
So, by AA rule of similarity △BMP ~ △CNP.
As triangles are similar,
Hence proved.
Answered By
Related Questions
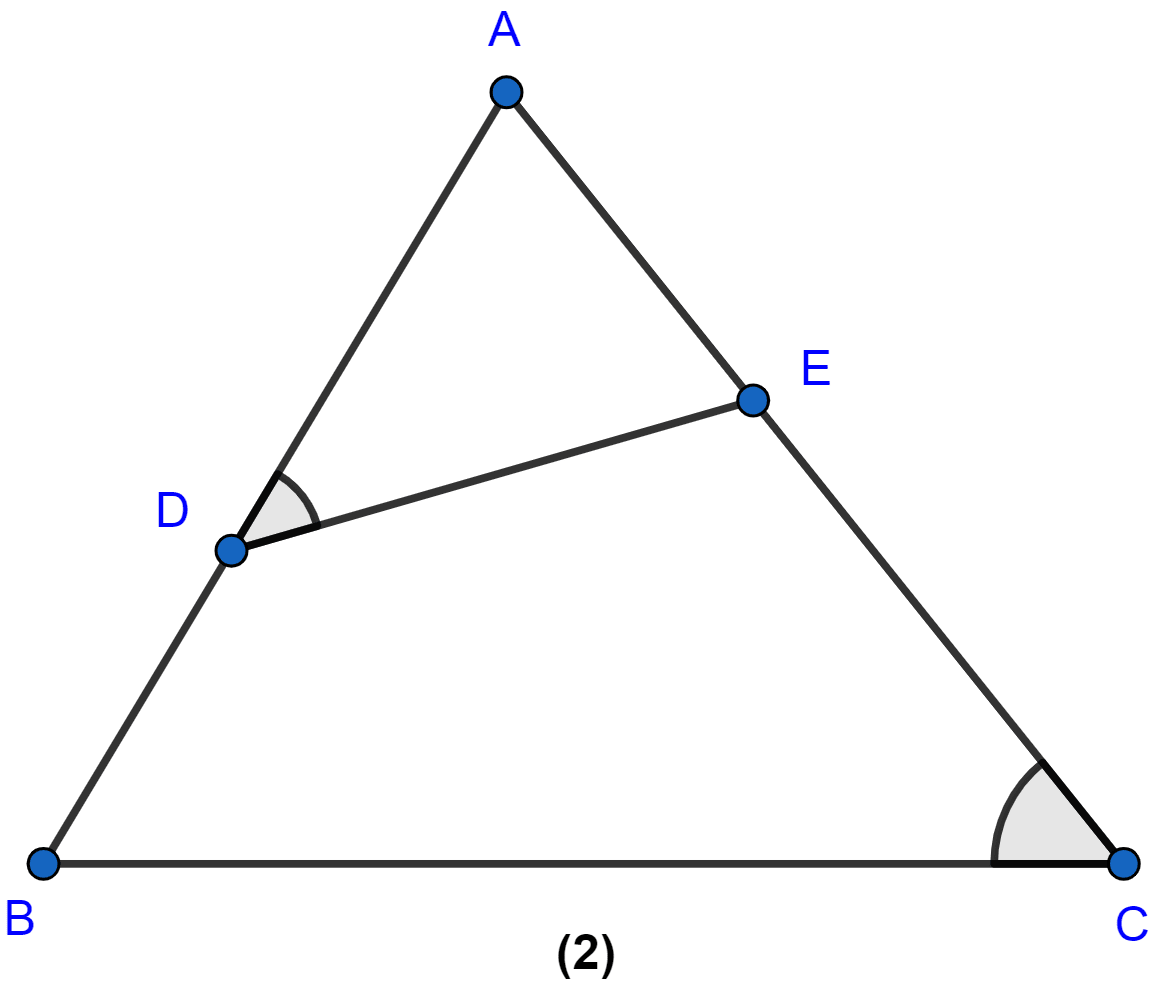
In the figure (2) given below, ∠ ADE = ∠ ACB.
(i) Prove that △s ABC and AED are similar.
(ii) If AE = 3 cm, BD = 1 cm and AB = 6 cm, calculate AC.
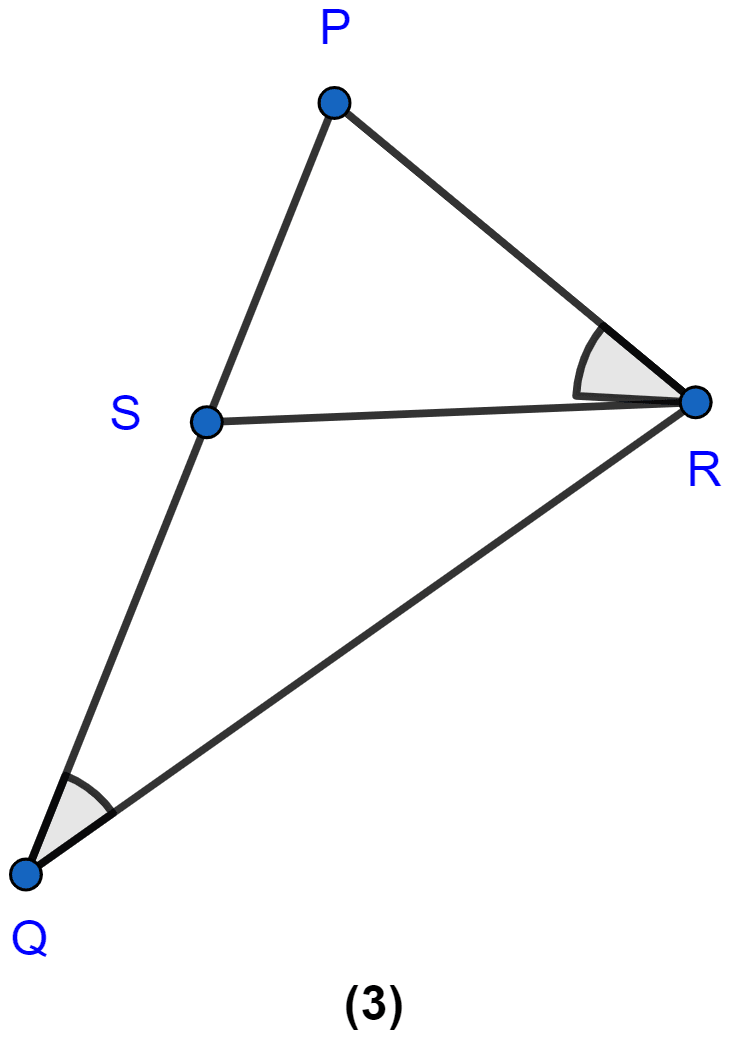
In the figure (3) given below, ∠ PQR = ∠ PRS. Prove that triangles PQR and PRS are similar. If PR = 8 cm, PS = 4 cm, calculate PQ.
Prove that the ratio of the perimeters of two similar triangles is the same as the ratio of their corresponding sides.
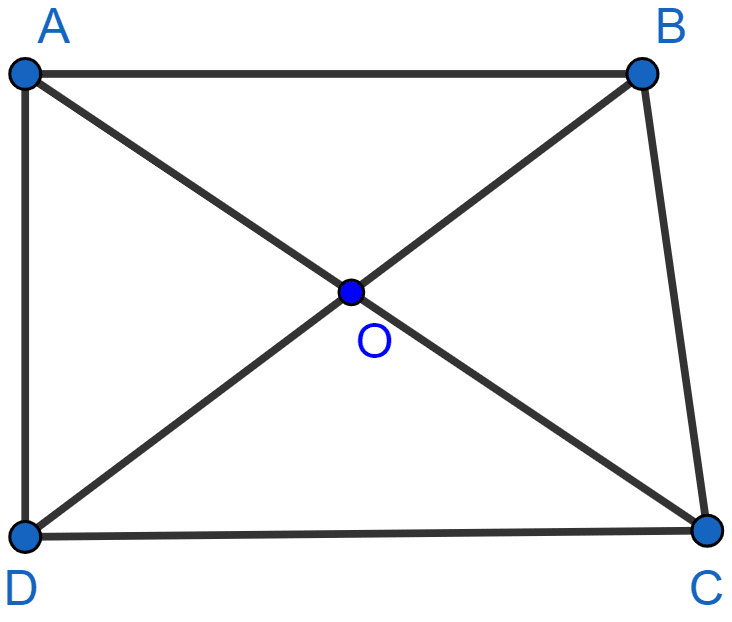
In the adjoining figure, ABCD is a trapezium in which AB ∥ DC. The diagonals AC and BD intersect at O. Prove that
Using the above result, find the value(s) of x if OA = 3x - 19, OB = x - 4, OC = x - 3 and OD = 4.