Mathematics
Prove that the ratio of the perimeters of two similar triangles is the same as the ratio of their corresponding sides.
Similarity
86 Likes
Answer
Let two similar triangles be △ABC and △PQR.
We know that when triangles are similar ratio of corresponding sides are equal.
By property of ratio i.e.,
if then each ratio = .
So,
Since, AB + BC + AC = Perimeter of △ABC and PQ + QR + PR = Perimeter of △PQR. So,
Hence, proved.
Answered By
48 Likes
Related Questions
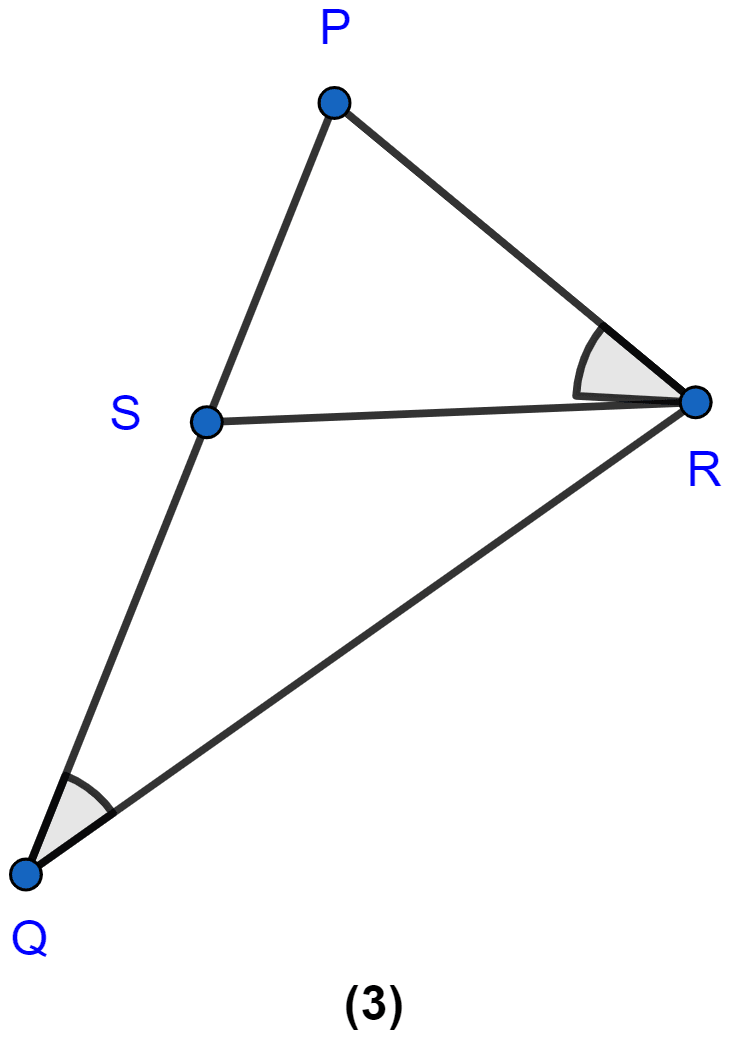
In the figure (3) given below, ∠ PQR = ∠ PRS. Prove that triangles PQR and PRS are similar. If PR = 8 cm, PS = 4 cm, calculate PQ.
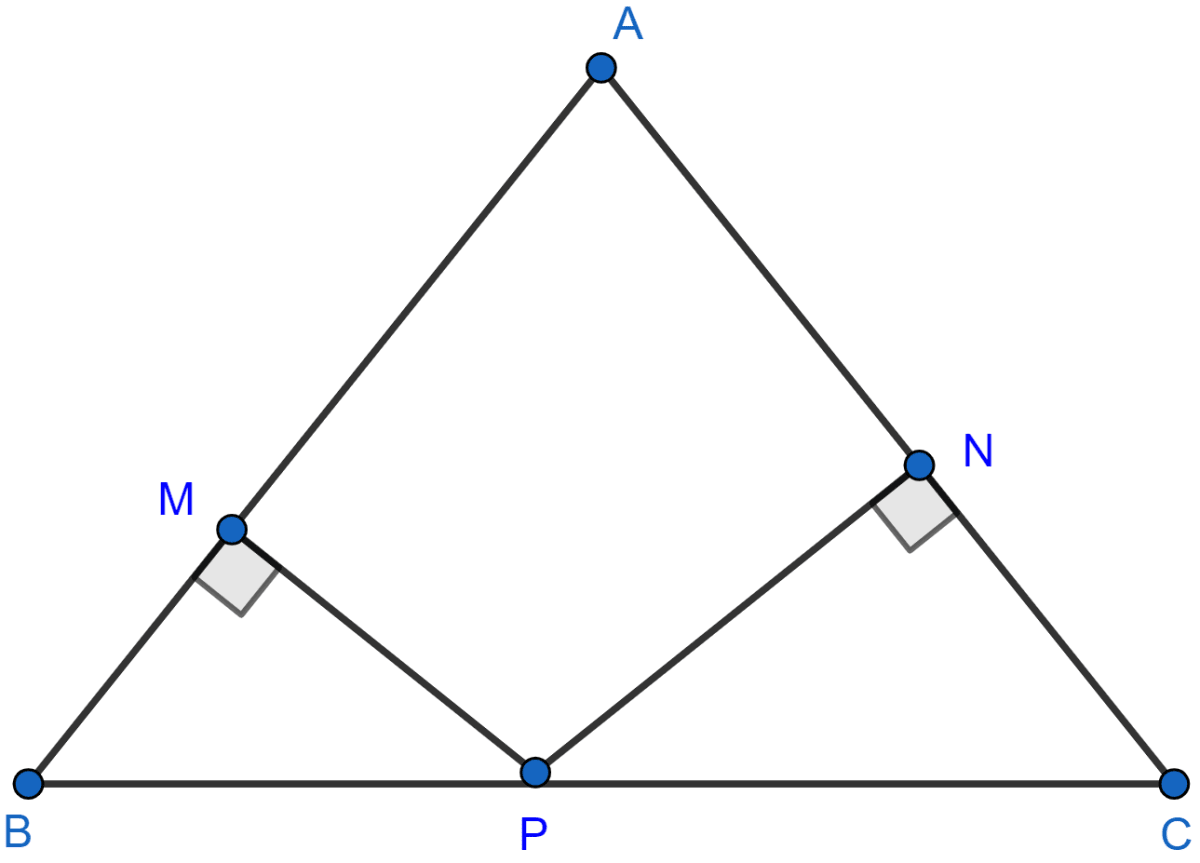
In the adjoining figure, ABC is a triangle in which AB = AC. P is a point on the side BC such that PM ⊥ AB and PN ⊥ AC. Prove that BM × NP = CN × MP.
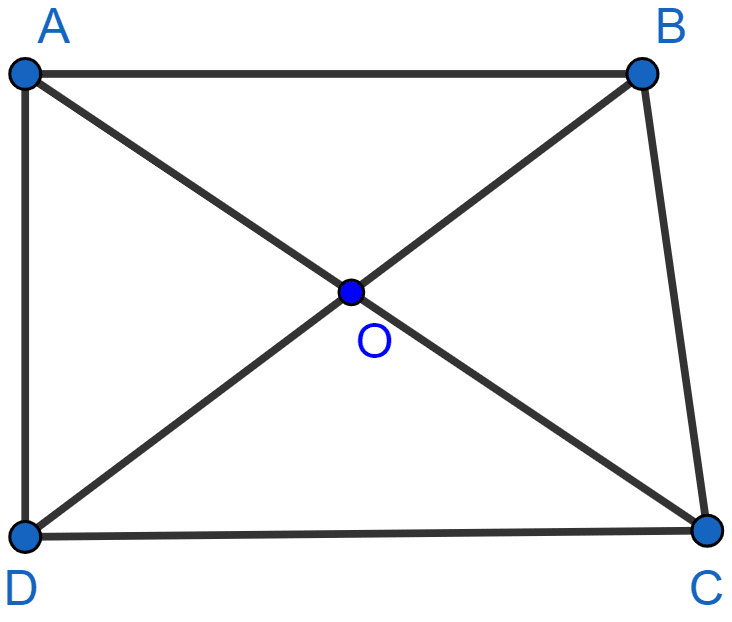
In the adjoining figure, ABCD is a trapezium in which AB ∥ DC. The diagonals AC and BD intersect at O. Prove that
Using the above result, find the value(s) of x if OA = 3x - 19, OB = x - 4, OC = x - 3 and OD = 4.
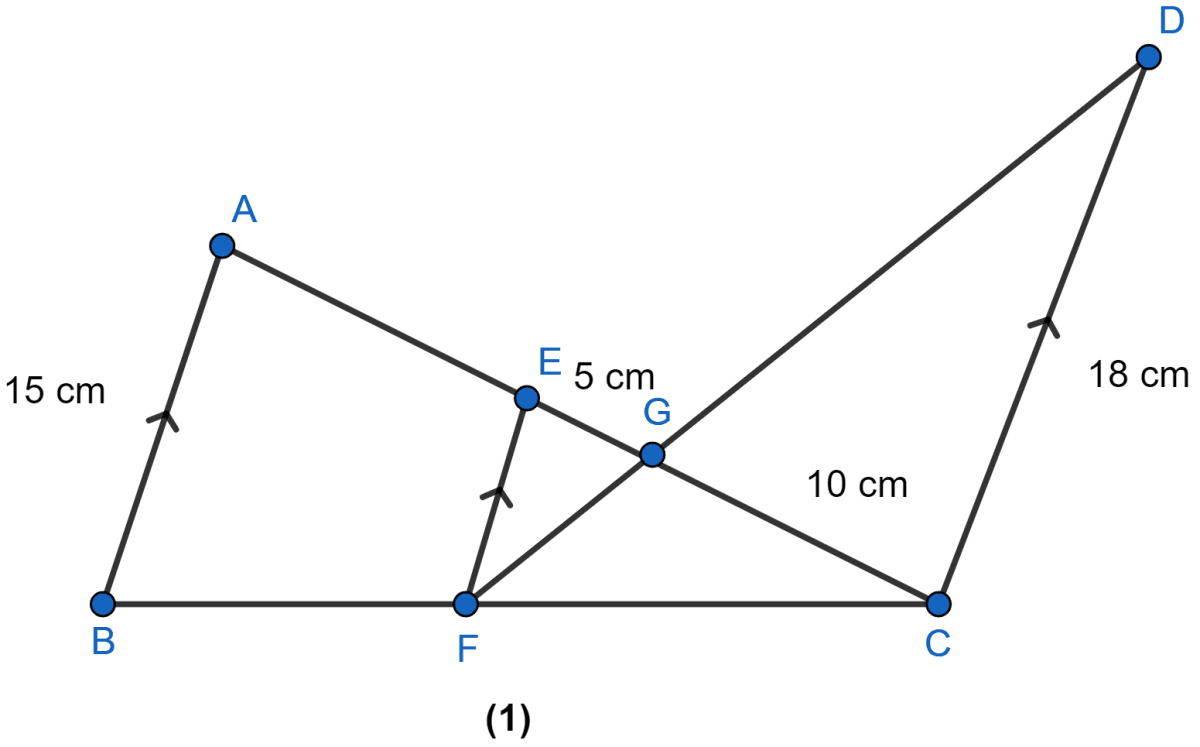
In the figure (1) given below, AB, EF and CD are parallel lines. Given that AB = 15 cm, EG = 5 cm, GC = 10 cm and DC = 18 cm. Calculate
(i) EF (ii) AC