In △ABC, A (3, 5), B (7, 8) and C (1, -10). Find the equation of the median through A.

Let AD be the median.

Since, AD is the median so D will be the mid-point of BC.

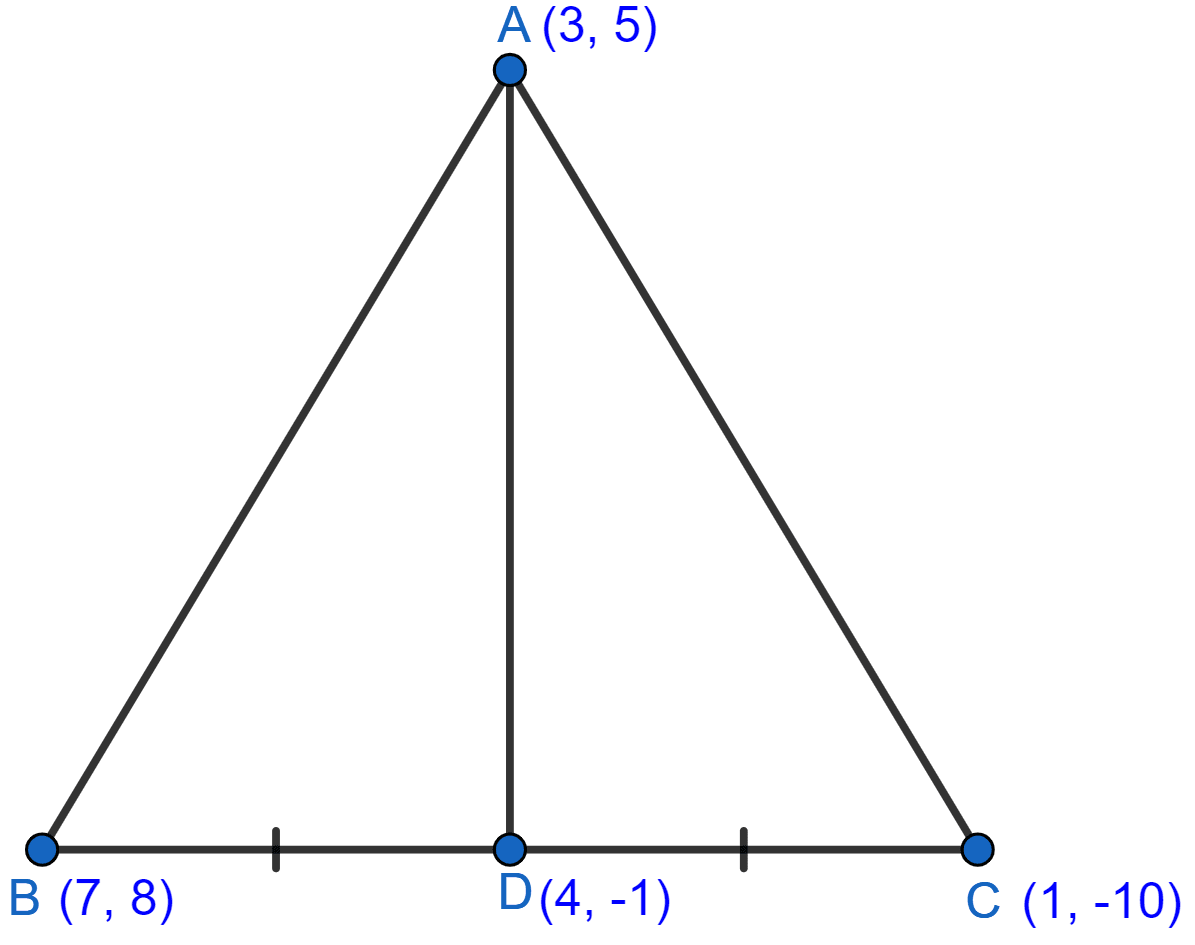
Co-ordinates of D = $\Big(\dfrac{7 + 1}{2}, \dfrac{8 + (-10)}{2}\Big) = \Big(\dfrac{8}{2}, \dfrac{-2}{2}\Big)$ = (4, -1).

$\text{Slope of AD } = \dfrac{y$2 - y1}{x2 - x1} \\[1em] = \dfrac{-1 - 5}{4 - 3} \\[1em] = \dfrac{-6}{1} \\[1em] = -6.

By point-slope form,

$y - y$1 = m(x - x1)

Substituting values we get,

⇒ y - 5 = -6(x - 3)

⇒ y - 5 = -6x + 18

⇒ y + 6x = 18 + 5

⇒ 6x + y = 23.

Hence, equation of median through A is 6x + y = 23.