Mathematics
In a triangle ABC, AD is perpendicular to BC. Prove that AB2 + CD2 = AC2 + BD2.
Answer
From figure,
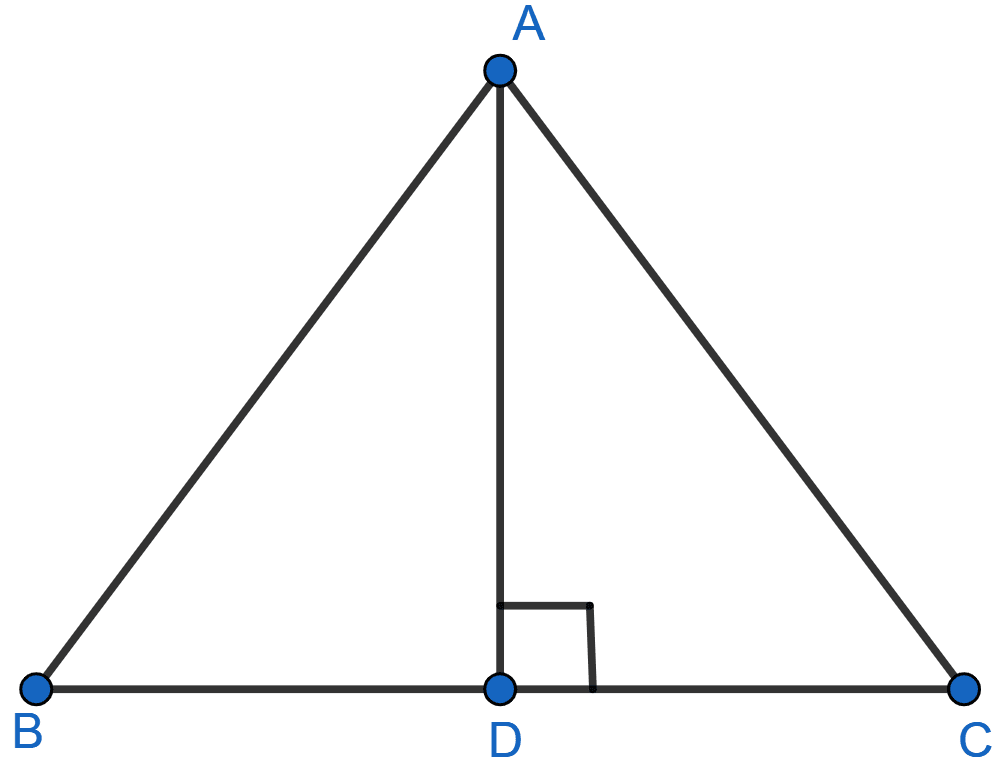
Considering right triangle ABD,
By pythagoras theorem,
AB2 = AD2 + BD2 …….(1)
Considering right triangle ACD,
By pythagoras theorem,
AC2 = AD2 + CD2 …….(2)
Subtracting eqn. 2 from 1 we get,
⇒ AB2 - AC2 = AD2 + BD2 - AD2 - CD2
⇒ AB2 - AC2 = BD2 - CD2
⇒ AB2 + CD2 = BD2 + AC2.
Hence, proved that AB2 + CD2 = AC2 + BD2.
Related Questions
The hypotenuse of a right triangle is 6 m more than twice the shortest side. If the third side is 2m less than the hypotenuse, find the sides of the triangle.
ABC is an isosceles triangle right angled at C. Prove that AB2 = 2AC2.
In △PQR, PD ⊥ QR such that D lies on QR. If PQ = a, PR = b, QD = c and DR = d, prove that (a + b)(a - b) = (c + d)(c - d).
ABC is an isosceles triangle with AB = AC = 12 cm and BC = 8 cm. Find the altitude on BC and hence calculate its area.