If two vertices of a parallelogram are (3, 2), (-1, 0) and its diagonals meet at (2, -5), find the other two vertices of the parallelogram.

The mid-point of the line segment joining the points (3, 2) and (-1, 0) is $\Big(\dfrac{3 + (-1)}{2}, \dfrac{2 + 0}{2}\Big)$ = (1, 1) which is not the same as (2, -5), therefore, the given points cannot be the opposite vertices. Hence, these vertices are adjoining.

The below figure shows the parallelogram:

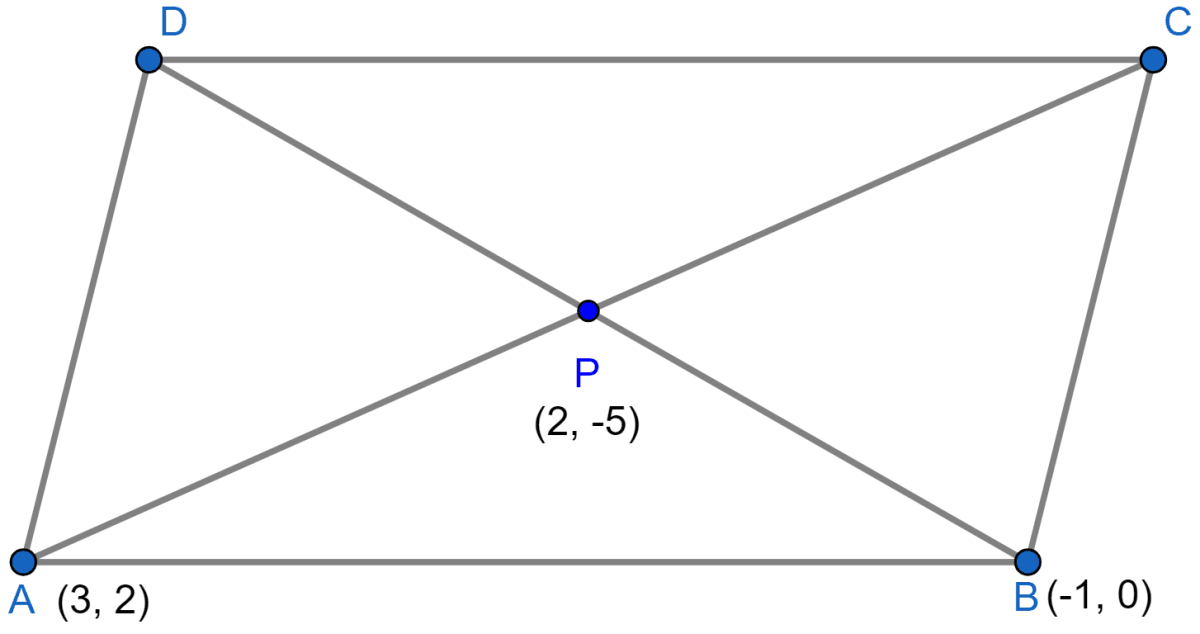
Let coordinates of C be (x, y) then by mid-point formula,

$\Rightarrow 2 = \dfrac{x + 3}{2} \text{ and} -5 = \dfrac{y + 2}{2}$
⇒ x + 3 = 4 and y + 2 = -10
⇒ x = 1 and y = -12.

∴ Coordinates of C are (1, -12).

Now finding coordinates of D, let D be (m, n). Applying mid-point formula we get,

$\Rightarrow 2 = \dfrac{m - 1}{2} \text{ and } -5 = \dfrac{n + 0}{2}$
⇒ m - 1 = 4 and n = -10
⇒ m = 5 and n = -10.

∴ Coordinates of D are (5, -10).

Hence, the coordinates of C are (1, -12) and D are (5, -10).