Find the third vertex of a triangle if its two vertices are (-1, 4) and (5, 2) and mid-point of one side is (0, 3).

Let A(-1, 4) and B(5, 2) be the two points and let C(x, y) be the third vertex of the triangle as shown in the figure below:

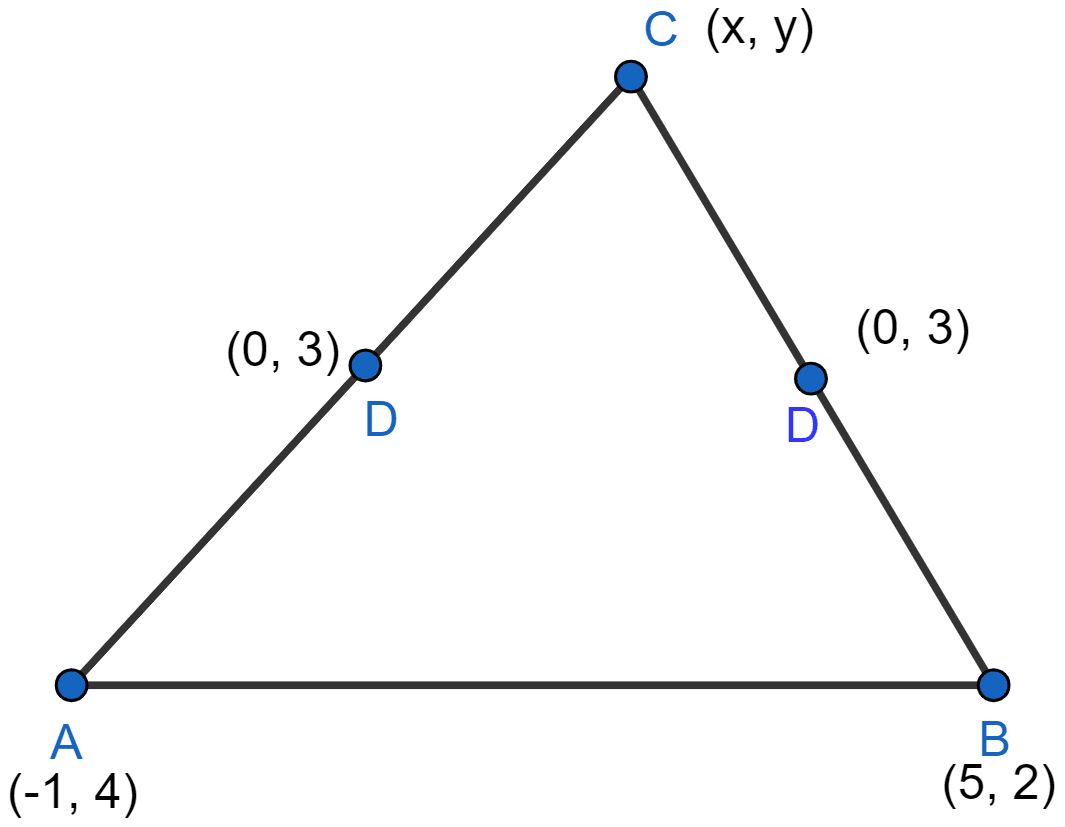
By mid-point formula, mid-point of AB

$= \Big(\dfrac{-1 + 5}{2}, \dfrac{4 + 2}{2}\Big) \\[1em] = \Big(\dfrac{4}{2}, \dfrac{6}{2}\Big) \\[1em] = (2, 3)$

Since, (0, 3) is not the mid-point of AB hence, it is either the mid point of AC or BC.

Let D(0, 3) be the midpoint of AC. So, by mid-point formula,

$0 = \dfrac{x + (-1)}{2} \text{ and } 3 = \dfrac{y + 4}{2}$
⇒ x - 1 = 0 and y + 4 = 6
⇒ x = 1 and y = 2.

∴ Coordinates of C will be (1, 2).

Let D(0, 3) be the midpoint of BC. So, by mid-point formula,

$0 = \dfrac{5 + x}{2} \text{ and } 3 = \dfrac{2 + y}{2}$
⇒ x + 5 = 0 and y + 2 = 6
⇒ x = -5 and y = 4.

∴ Coordinates of C will be (-5, 4).

Hence, the coordinates of C will be (1, 2) or (-5, 4).