Mathematics
If two vertices of a parallelogram are (3, 2), (-1, 0) and its diagonals meet at (2, -5), find the other two vertices of the parallelogram.
Section Formula
30 Likes
Answer
The mid-point of the line segment joining the points (3, 2) and (-1, 0) is = (1, 1) which is not the same as (2, -5), therefore, the given points cannot be the opposite vertices. Hence, these vertices are adjoining.
The below figure shows the parallelogram:
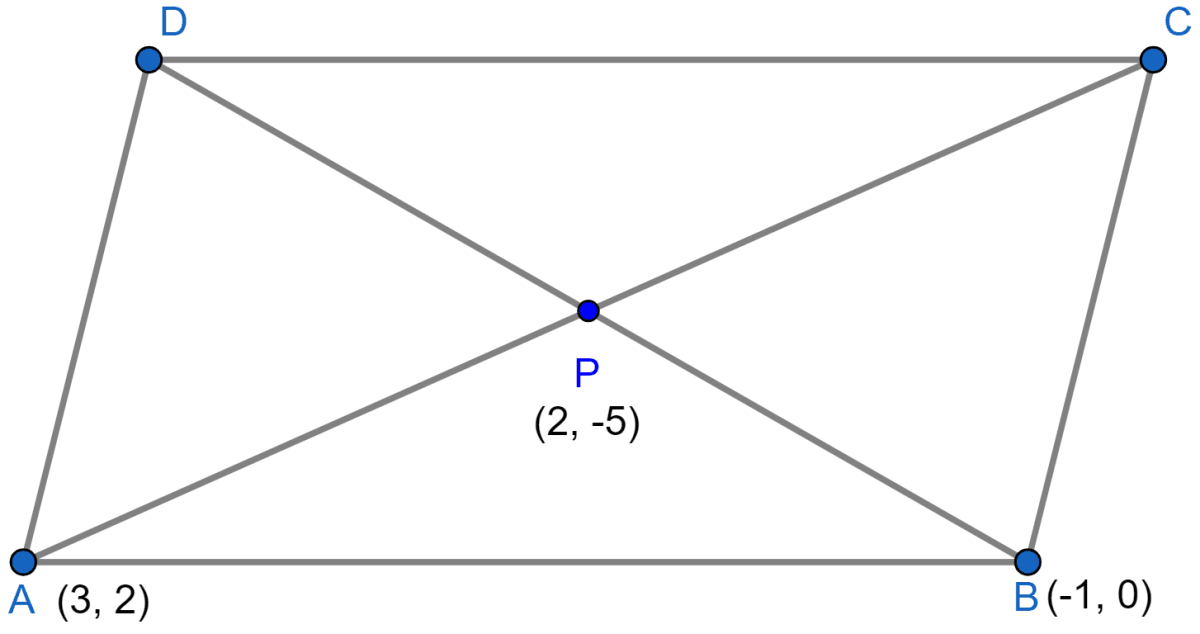
Let coordinates of C be (x, y) then by mid-point formula,
⇒ x + 3 = 4 and y + 2 = -10
⇒ x = 1 and y = -12.
∴ Coordinates of C are (1, -12).
Now finding coordinates of D, let D be (m, n). Applying mid-point formula we get,
⇒ m - 1 = 4 and n = -10
⇒ m = 5 and n = -10.
∴ Coordinates of D are (5, -10).
Hence, the coordinates of C are (1, -12) and D are (5, -10).
Answered By
18 Likes
Related Questions
Three consecutive vertices of a parallelogram ABCD are A(1, 2), B(1, 0) and C(4, 0). Find the fourth vertex D.
If the points A(-2, -1), B(1, 0), C(p, 3) and D(1, q) form a parallelogram ABCD, find the values of p and q.
Find the third vertex of a triangle if its two vertices are (-1, 4) and (5, 2) and mid-point of one side is (0, 3).
Find the coordinates of the vertices of the triangle, the middle points of whose sides are .