Find the coordinates of the vertices of the triangle, the middle points of whose sides are $\Big(0, \dfrac{1}{2}\Big), \Big(\dfrac{1}{2}, \dfrac{1}{2}\Big) \text{ and } \Big(\dfrac{1}{2}, 0\Big)$.

Let ABC be a triangle in which D, E and F are the mid-points of sides AB, BC and CA respectively.

Let coordinates of A be (x₁, y₁), B(x₂, y₂), C(x₃, y₃).

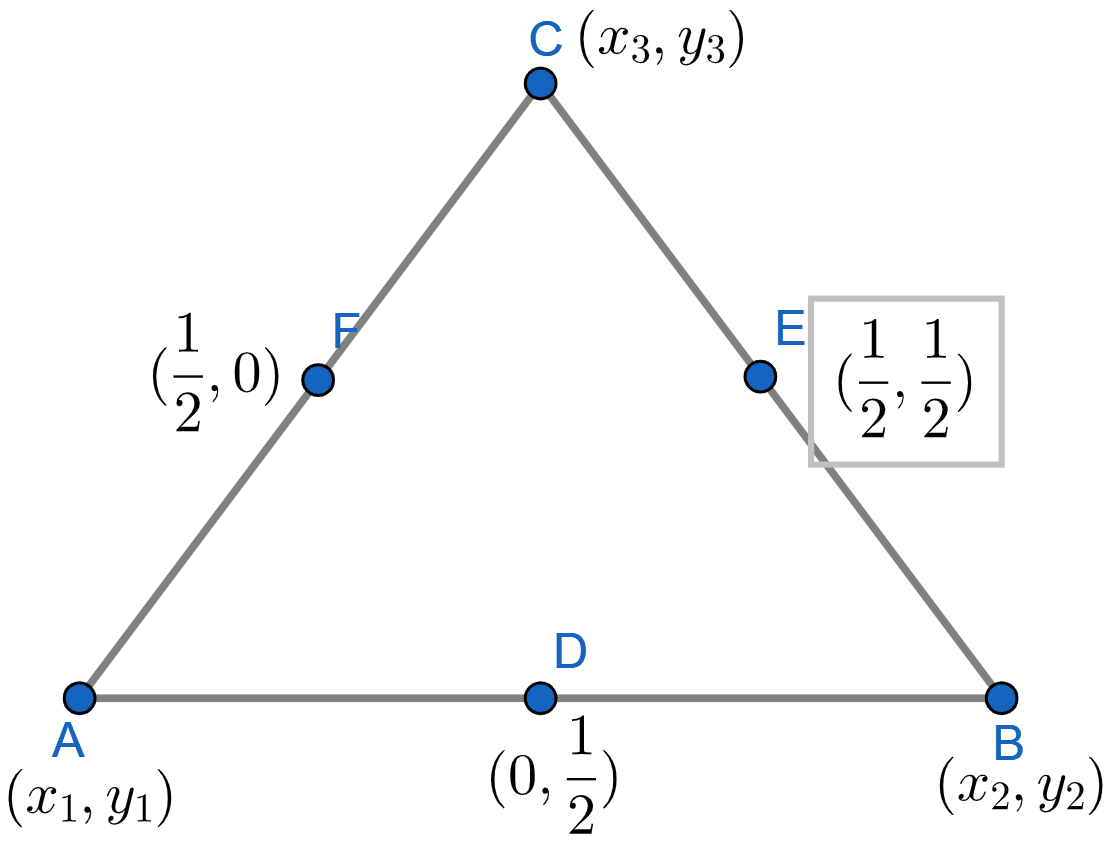
Applying mid-point formula on side AB,

$0 = \dfrac{x$1 + x2}{2} \\[1em] \Rightarrow x1 + x2 = 0 \qquad \text{….[Eq 1]} \\[1.5em] \dfrac{1}{2} = \dfrac{y1 + y2}{2} \\[1em] \Rightarrow y1 + y2 = 1 \qquad \text{….[Eq 2]} \\[1em]

Applying mid-point formula on side BC,

$\dfrac{1}{2} = \dfrac{x$2 + x3}{2} \\[1em] \Rightarrow x2 + x3 = 1. \qquad \text{….[Eq 3]} \\[1em] \dfrac{1}{2} = \dfrac{y2 + y3}{2} \\[1em] \Rightarrow y2 + y3 = 1 \qquad \text{….[Eq 4]} \\[1em]

Applying mid-point formula on side CA,

$\dfrac{1}{2} = \dfrac{x$3 + x1}{2} \\[1em] \Rightarrow x3 + x1 = 1. \qquad \text{….[Eq 5]} \\[1em] 0 = \dfrac{y3 + y1}{2} \\[1em] \Rightarrow y3 + y1 = 0 \qquad \text{….[Eq 6]} \\[1em]

Adding Eq 1, 3 and 5,

$x$1 + x2 + x2 + x3 + x3 + x1 = 0 + 1 + 1.
∴ x₁ + x₂ + x₃ = 1. $\qquad \text{….[Eq 7]}$

On subtracting Eq 3 from Eq 7 we get,
x₁ + x₂ + x₃ - (x₂ + x₃) = 1 - 1
x₁ + x₂ + x₃ - x₂ - x₃ = 0
x₁ = 0.

On subtracting Eq 5 from Eq 7 we get,
x₁ + x₂ + x₃ - (x₃ + x₁) = 1 - 1
x₁ + x₂ + x₃ - x₃ - x₁ = 0
x₂ = 0.

On subtracting Eq 1 from Eq 7 we get,
x₁ + x₂ + x₃ - (x₁ + x₂) = 1 - 0
x₁ + x₂ + x₃ - x₁ - x₂ = 1
x₃ = 1.

Adding Eq 2, 4 and 5,

$y$1 + y2 + y2 + y3 + y3 + y1 = 1 + 1 + 0.
∴ y₁ + y₂ + y₃ = 1. (Eq 8)

On subtracting Eq 4 from Eq 8 we get,
y₁ + y₂ + y₃ - (y₂ + y₃) = 1 - 1
y₁ + y₂ + y₃ - y₂ - y₃ = 0
y₁ = 0.

On subtracting Eq 6 from Eq 8 we get,
y₁ + y₂ + y₃ - (y₃ + y₁) = 1 - 0
y₁ + y₂ + y₃ - y₃ - y₁ = 1
y₂ = 1.

On subtracting Eq 2 from Eq 8 we get,
y₁ + y₂ + y₃ - (y₁ + y₂) = 1 - 1
y₁ + y₂ + y₃ - y₁ - y₂ = 1 - 1
y₃ = 0.

Hence, coordinates of vertices of triangle are (0, 0), (0, 1) and (1, 0) respectively.