Three consecutive vertices of a parallelogram ABCD are A(1, 2), B(1, 0) and C(4, 0). Find the fourth vertex D.

In the parallelogram ABCD, the three consecutive vertices are A(1, 2), B(1, 0) and C(4, 0). Let the fourth vertex D be (x, y) as shown in the figure below:

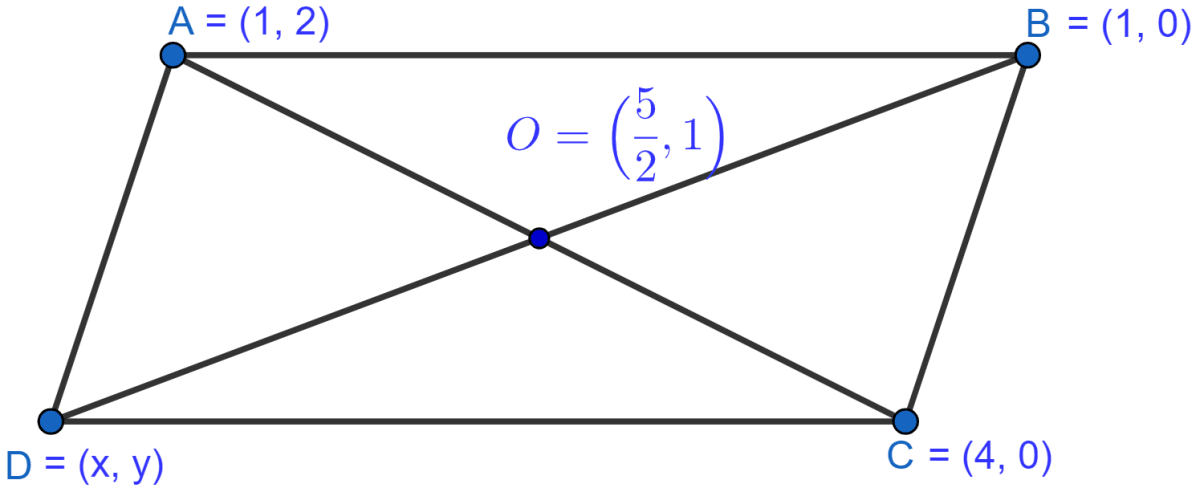
Let O be the mid-point of AC, the diagonal of ABCD.

By Mid-point formula, the coordinates of O = $\Big(\dfrac{1 + 4}{2}, \dfrac{2 + 0}{2}\Big)$

∴ Coordinates of O will be $\Big(\dfrac{5}{2}, 1\Big)$

The mid-point of BD is $\Big(\dfrac{1 + x}{2}, \dfrac{y}{2}\Big)$

Since, the diagonals of a parallelogram bisect each other, the mid-points of AC and BD are same.

$\therefore \dfrac{5}{2} = \dfrac{1 + x}{2} \text{ and } 1 = \dfrac{0 + y}{2} \\[1em] \Rightarrow 5 = 1 + x \text{ and } y + 0 = 2 \\[1em] \Rightarrow x = 5 - 1 \text{ and } y = 2. \\[1em] \Rightarrow x = 4 \text{ and } y = 2.$

Hence, coordinates of D are (4, 2).