Mathematics
If two sides of a cyclic-quadrilateral are parallel; prove that :
(i) its other two sides are equal.
(ii) its diagonals are equal.
Answer
Let ABCD is a cyclic quadrilateral in which AB || DC. AC and BD are its diagonals.
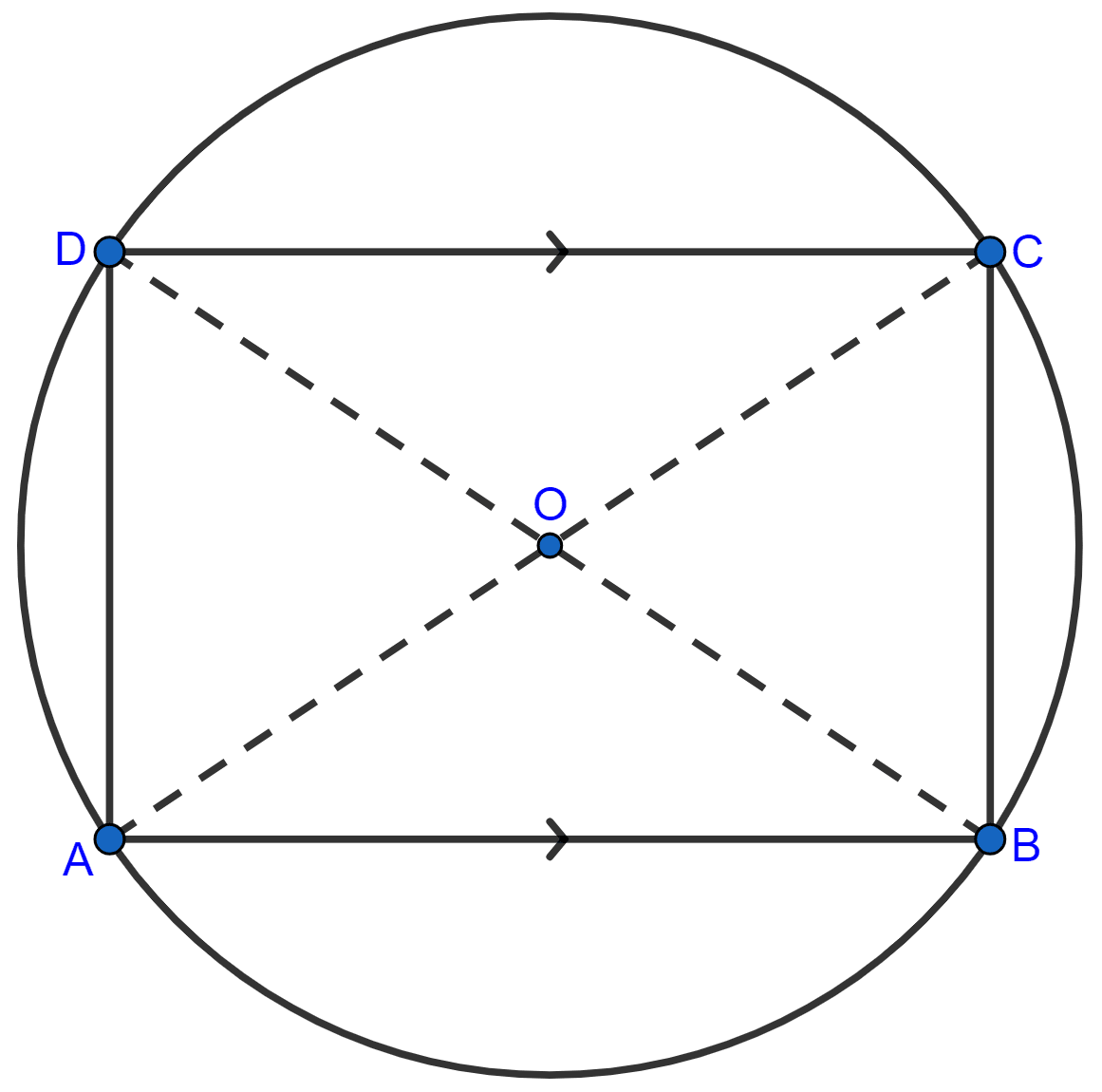
As AB || DC (given)
∠DCA = ∠CAB [Alternate angles are equal]
Chord AD subtends ∠DCA and chord BC subtends ∠CAB at the circumference of the circle.
and
∠DCA = ∠CAB
We know that,
If the angles subtended by 2 chords on the circumference of the circle are equal, then the lengths of the chords are also equal.
∴ chord AD = chord BC or AD = BC.
Hence, proved that AD = BC.
(ii) From figure,
⇒ ∠A + ∠C = 180° [As, sum of opposite angles in a cyclic quadrilateral = 180°]
Also,
⇒ ∠B + ∠C = 180° [Sum of co-interior angles = 180° (As, AB || CD)]
∴ ∠B + ∠C = ∠A + ∠C
⇒ ∠B = ∠A
In ∆ABC and ∆ADB
⇒ AB = AB [Common]
⇒ ∠B = ∠A [Proved above]
⇒ BC = AD [Proved above]
Hence, by SAS criterion of congruence
∆ACB ≅ ∆ADB
∴ AC = BD [By C.P.C.T.]
Hence, proved that AC = BC.
Related Questions
In a cyclic-trapezium, the non-parallel sides are equal and the diagonals are also equal. Prove it.
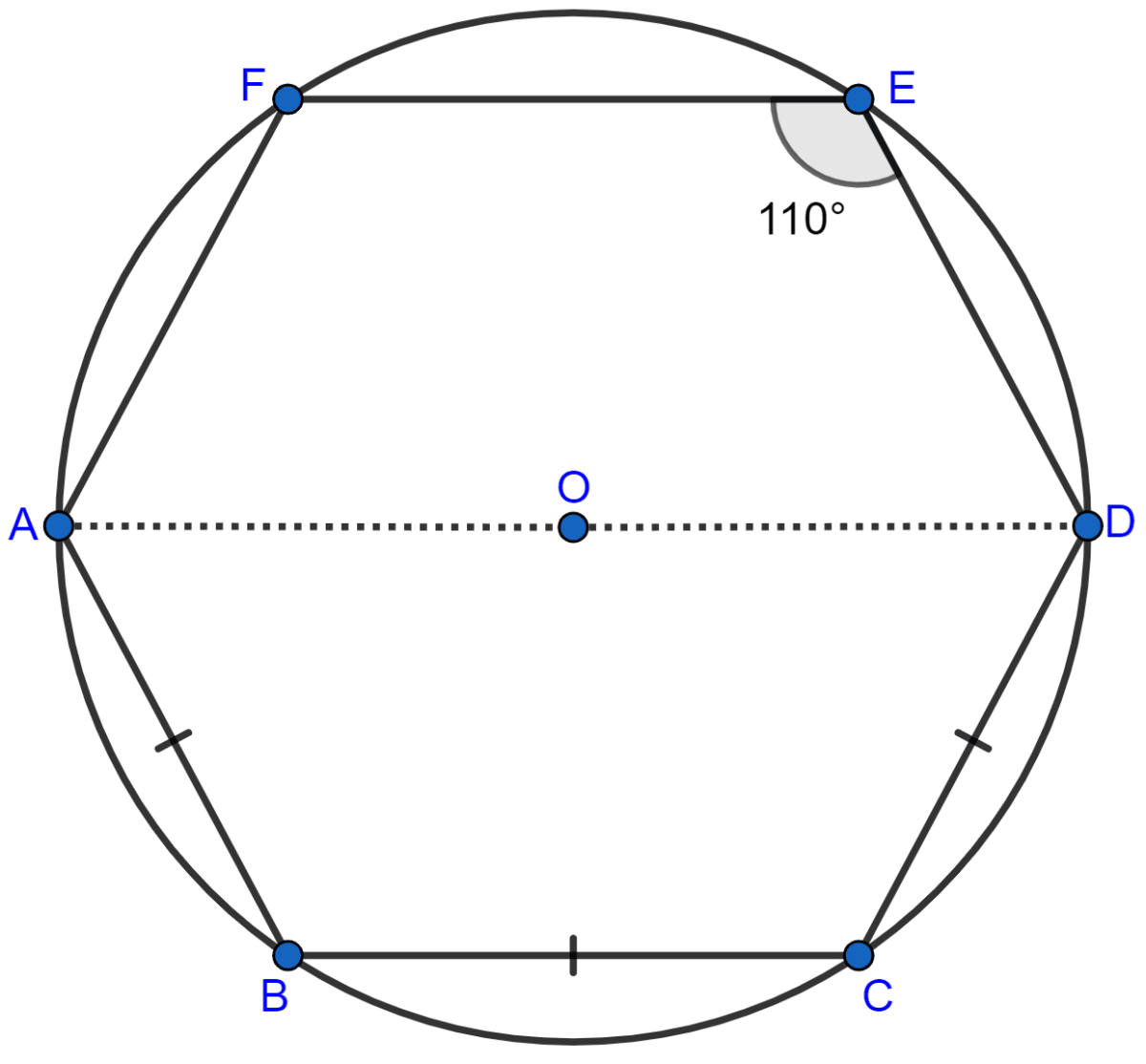
In the following figure, AD is the diameter of the circle with centre O. Chords AB, BC and CD are equal. If ∠DEF = 110°, calculate :
(i) ∠AEF, (ii) ∠FAB.
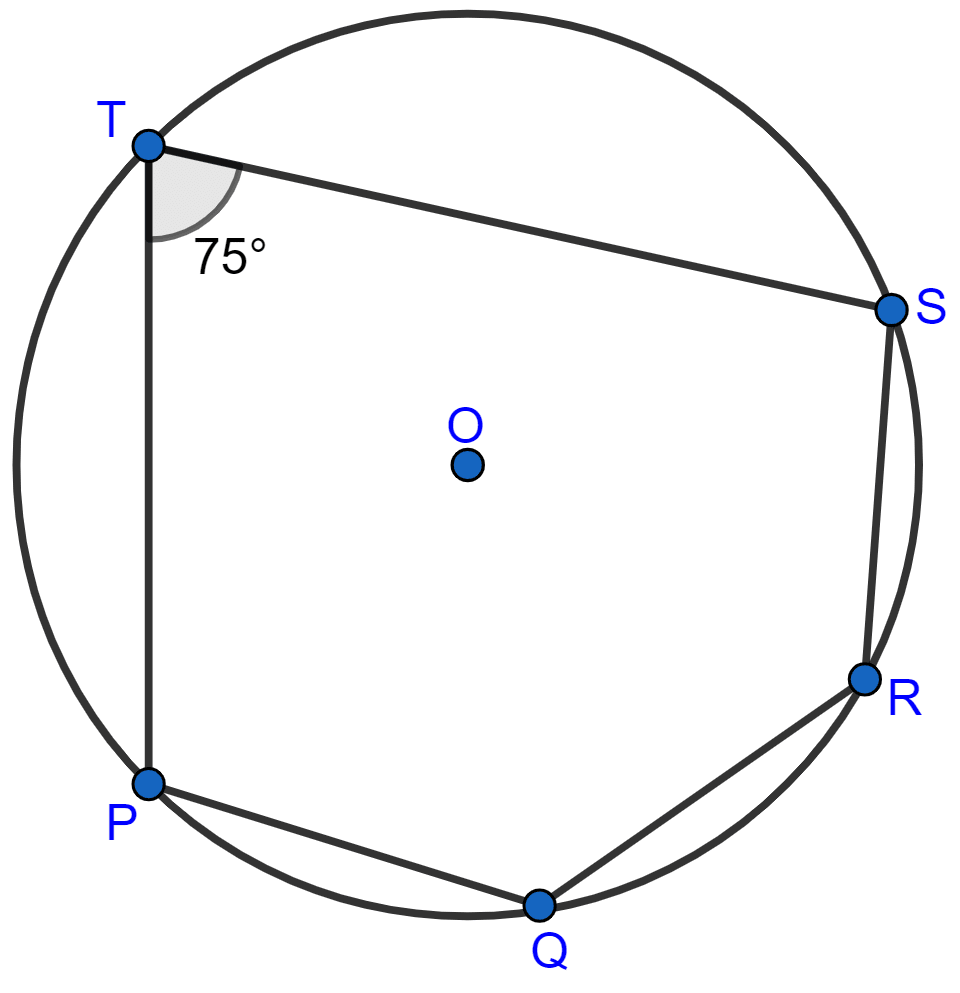
The given figure show a circle with centre O. Also, PQ = QR = RS and ∠PTS = 75°.
Calculate:
(i) ∠POS,
(ii) ∠QOR,
(iii) ∠PQR.
In the given figure, AB is a side of a regular six-sided polygon and AC is a side of a regular eight-sided polygon inscribed in the circle with centre O. Calculate the sizes of :
(i) ∠AOB,
(ii) ∠ACB,
(iii) ∠ABC.