Mathematics
In a cyclic-trapezium, the non-parallel sides are equal and the diagonals are also equal. Prove it.
Circles
20 Likes
Answer
Let ABCD be the cyclic trapezium in which AB || DC, AC and BD are the diagonals.
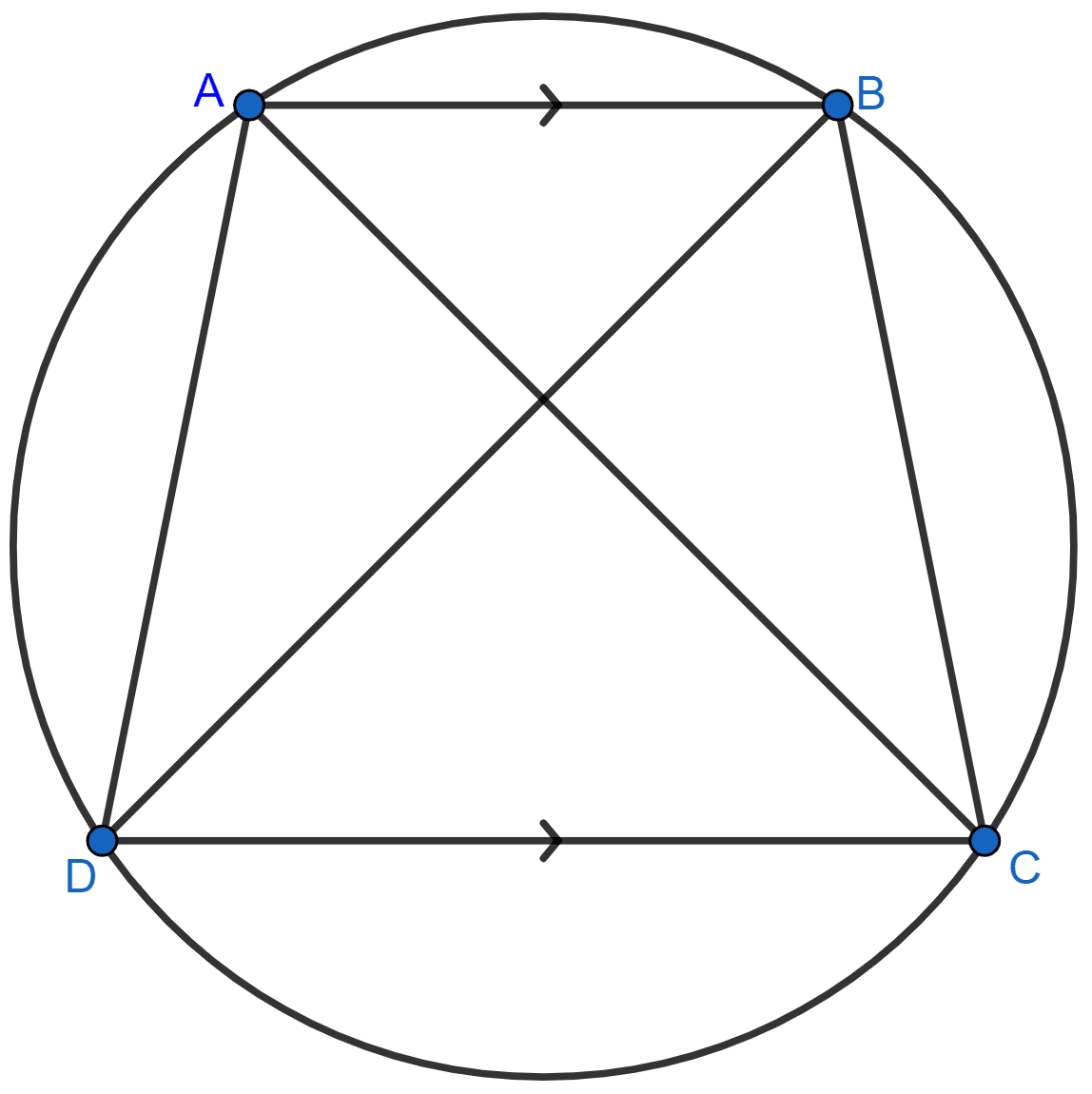
It's seen that chord AD subtends ∠ABD and chord BC subtends ∠BDC at the circumference of the circle.
But, ∠ABD = ∠BDC [Alternate angles, as AB || DC with BD as the transversal]
∴ Chord AD must be equal to chord BC [As equal chord subtends equal angles at circumference]
From figure,
⇒ ∠B + ∠D = 180° [As, sum of opposite angles in a cyclic quadrilateral = 180°]
Also,
⇒ ∠B + ∠C = 180° [Sum of co-interior angles = 180° (As, AB || CD)]
∴ ∠B + ∠C = ∠B + ∠D
⇒ ∠C = ∠D
Now, in ∆ADC and ∆BCD
⇒ DC = DC [Common]
⇒ ∠C = ∠D [Proved above]
⇒ AD = BC [Proved above]
Hence, by SAS criterion of congruence
∆ADC ≅ ∆BCD
∴ AC = BD [By C.P.C.T.]
Hence, proved above AC = BD and AD = BC.
Answered By
14 Likes
Related Questions
In the given figure, O is the center of the circle, AB is side of a regular pentagon, then angle ACB is equal to :
36°
72°
50°
40°

In the given figure, O is the center of the circle, chords AB, CD and EF are equal whereas chords BC, DE and FA are separately equal. The angle AOC is equal to :
80°
100°
90°
120°
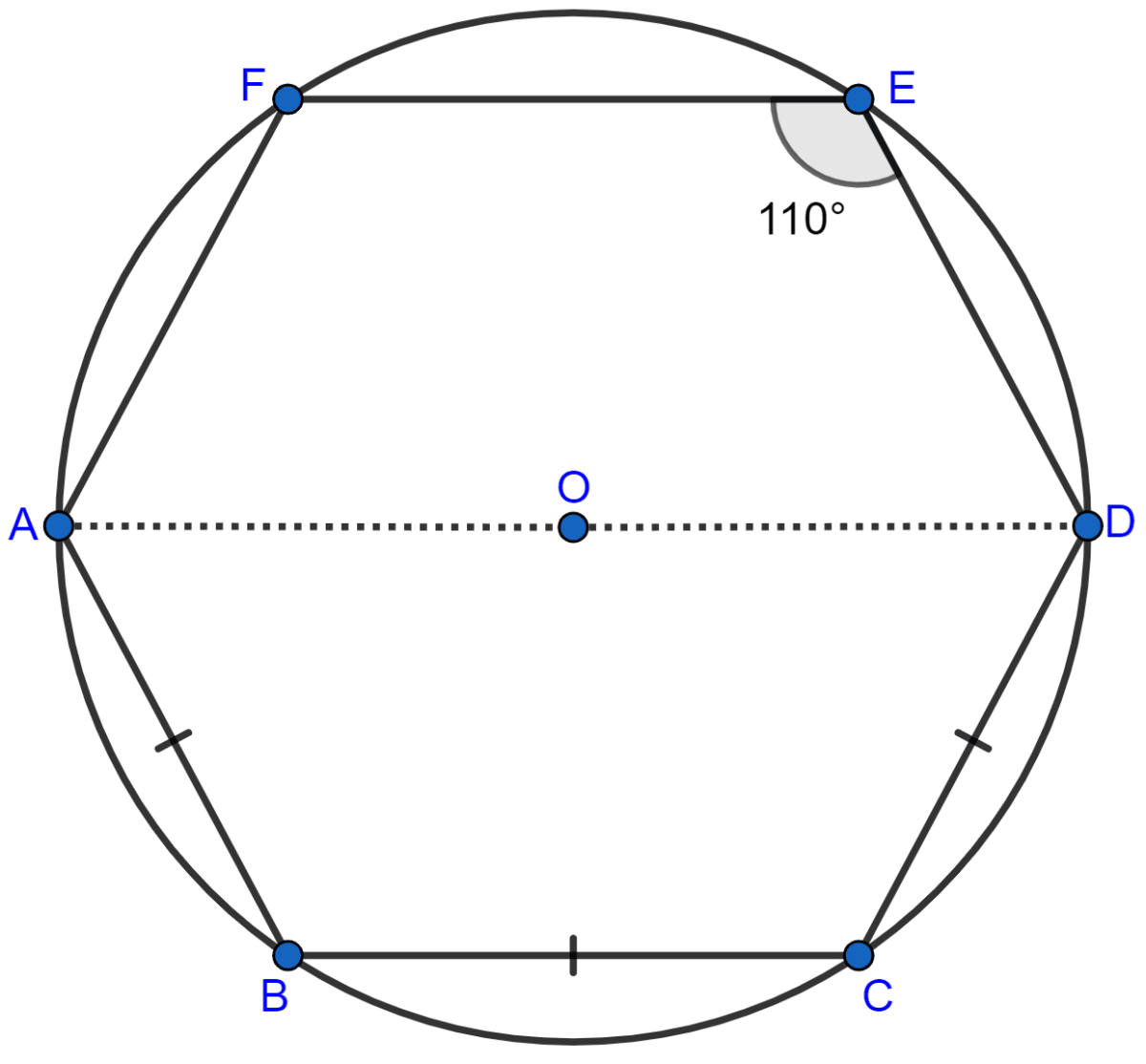
In the following figure, AD is the diameter of the circle with centre O. Chords AB, BC and CD are equal. If ∠DEF = 110°, calculate :
(i) ∠AEF, (ii) ∠FAB.
If two sides of a cyclic-quadrilateral are parallel; prove that :
(i) its other two sides are equal.
(ii) its diagonals are equal.