Mathematics
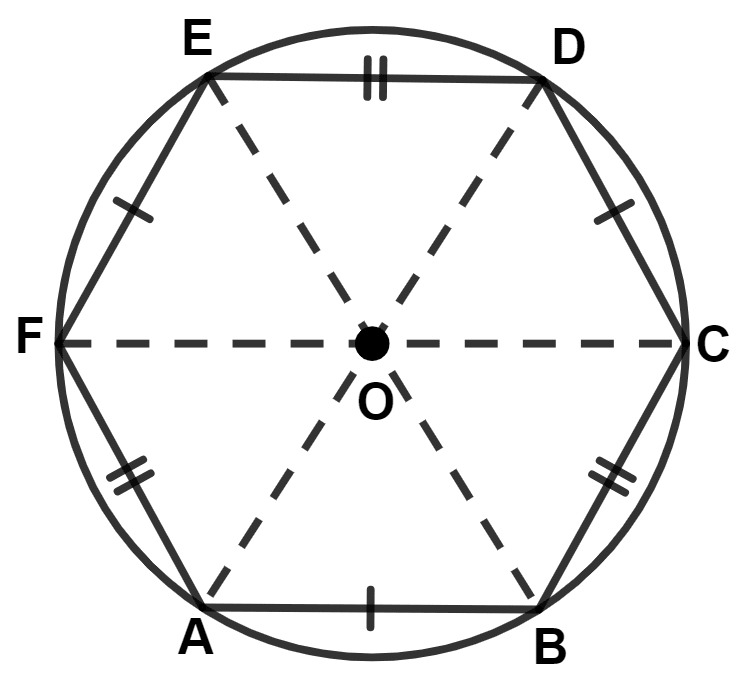
In the given figure, O is the center of the circle, chords AB, CD and EF are equal whereas chords BC, DE and FA are separately equal. The angle AOC is equal to :
80°
100°
90°
120°
Circles
10 Likes
Answer
Given,
Chords AB, CD and EF are equal.
∴ ∠AOB = ∠COD = ∠EOF = x (let)
Chords BC, DE and FA are equal.
∴ ∠BOC = ∠DOE = ∠AOF = y (let)
From figure,
⇒ ∠AOB + ∠COD + ∠EOF + ∠BOC + ∠DOE + ∠AOF = 360°
⇒ x + x + x + y + y + y = 360°
⇒ 3x + 3y = 360°
⇒ 3(x + y) = 360°
⇒ x + y =
⇒ x + y = 120°
From figure,
∠AOC = ∠AOB + ∠BOC = x + y = 120°.
Hence, Option 4 is the correct option.
Answered By
6 Likes
Related Questions
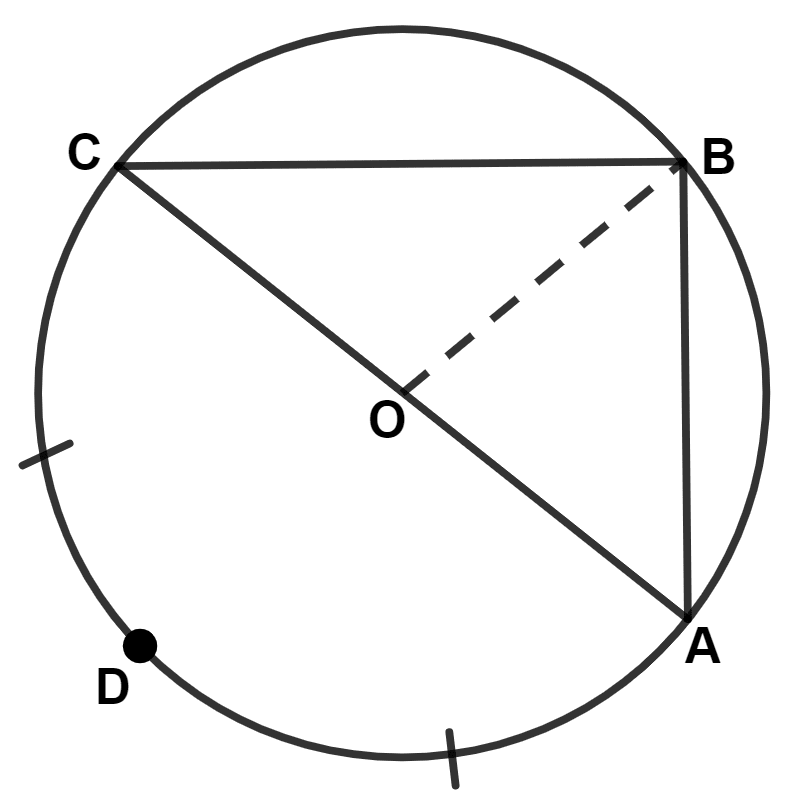
In the given figure, O is the center of a circle. AB is the side of a square and BC is side of a regular hexagon. Also arc AD = arc CD. Angle DOC is equal to :
150°
105°
130°
210°
In the given figure, O is the center of the circle, AB is side of a regular pentagon, then angle ACB is equal to :
36°
72°
50°
40°

In a cyclic-trapezium, the non-parallel sides are equal and the diagonals are also equal. Prove it.
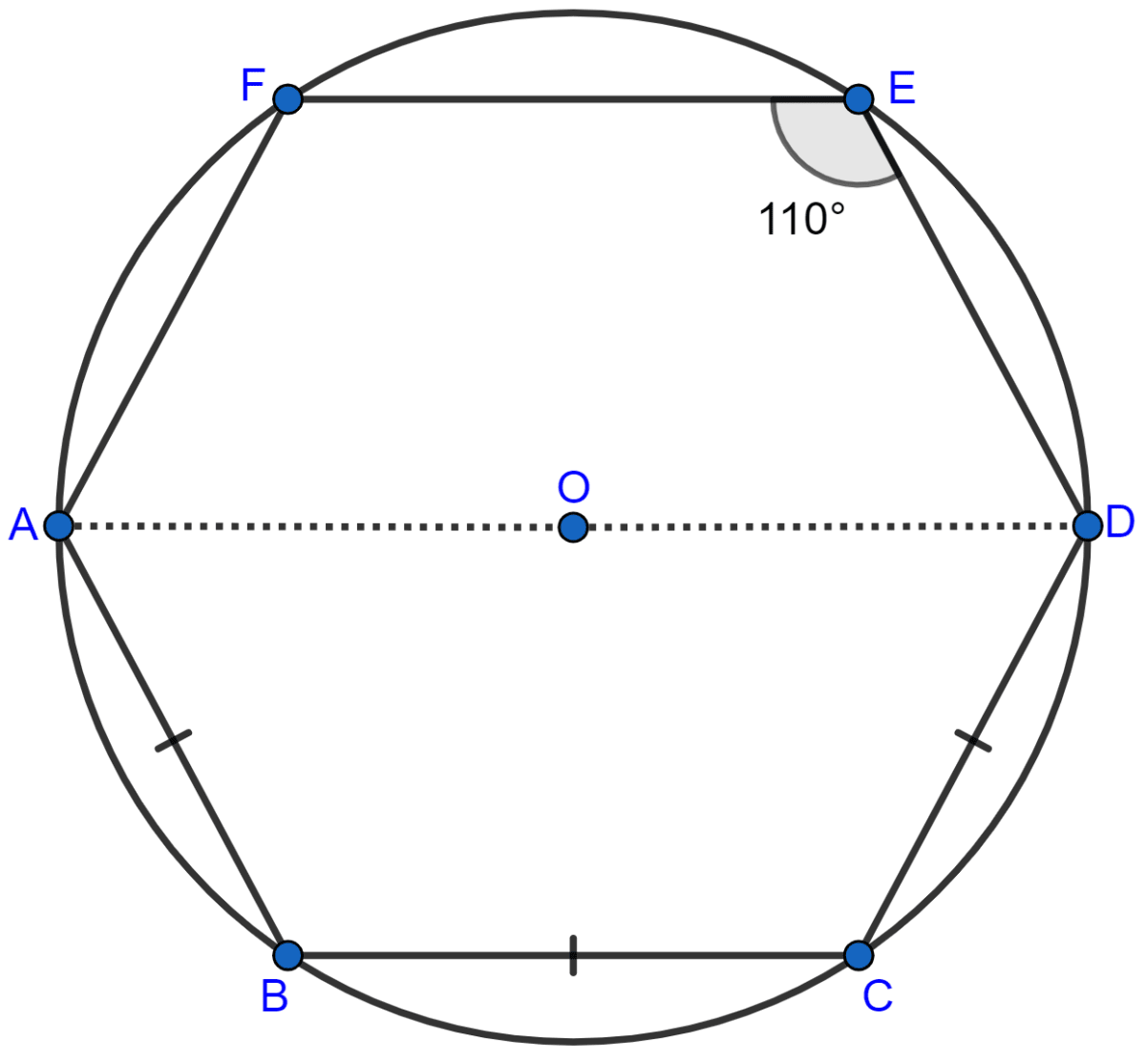
In the following figure, AD is the diameter of the circle with centre O. Chords AB, BC and CD are equal. If ∠DEF = 110°, calculate :
(i) ∠AEF, (ii) ∠FAB.