Mathematics
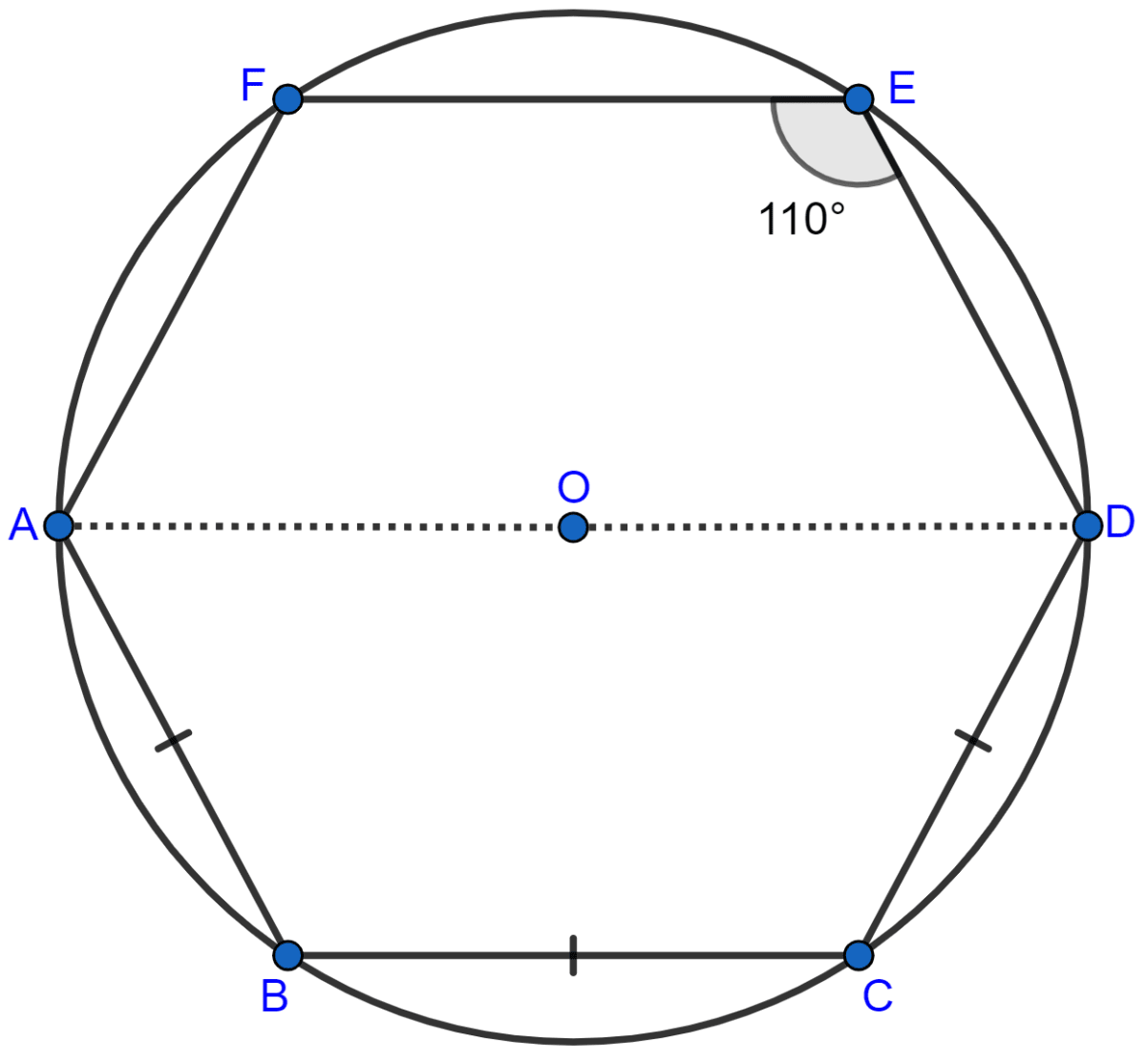
In the following figure, AD is the diameter of the circle with centre O. Chords AB, BC and CD are equal. If ∠DEF = 110°, calculate :
(i) ∠AEF, (ii) ∠FAB.
Circles
17 Likes
Answer
Join AE, OB and OC.
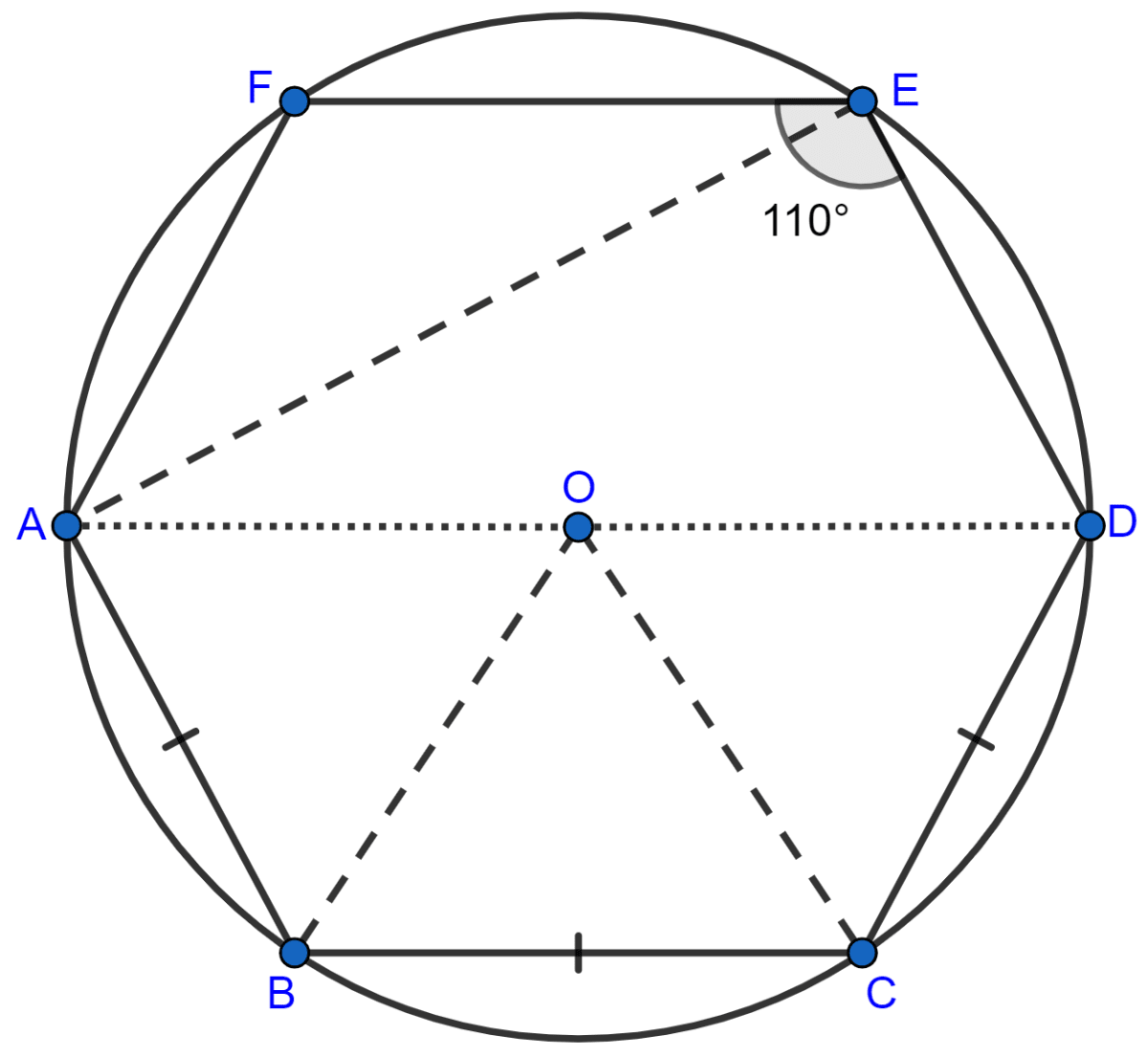
(i) As AOD is the diameter
∠AED = 90° [Angle in a semi-circle is a right angle]
But, given ∠DEF = 110°
So,
∠AEF = ∠DEF - ∠AED = 110° - 90° = 20°.
Hence, ∠AEF = 20°.
(ii) Also given, Chord AB = Chord BC = Chord CD
So,
∠AOB = ∠BOC = ∠COD [Equal chords subtends equal angles at the centre]
From figure,
⇒ ∠AOB + ∠BOC + ∠COD = 180° [AOD is a straight line]
⇒ ∠AOB = ∠BOC = ∠COD = = 60°
Now, in ∆OAB we have
OA = OB [Radii of same circle]
So, ∠OAB = ∠OBA [Angles opposite to equal sides are equal]
In ∆OAB,
⇒ ∠OAB + ∠OBA + ∠AOB = 180° [By angle sum property of triangle]
⇒ ∠OAB + ∠OBA + 60° = 180°
⇒ ∠OAB + ∠OBA = 180° - 60° = 120°.
Since, ∠OAB = ∠OBA
∴ ∠OAB = ∠OBA = = 60°.
Now, in cyclic quadrilateral ADEF
⇒ ∠DEF + ∠DAF = 180° [As sum of opposite angles in cyclic quadrilateral = 180°]
⇒ ∠DAF = 180° - ∠DEF
⇒ ∠DAF = 180° - 110° = 70°.
From figure,
∠FAB = ∠DAF + ∠OAB = 70° + 60° = 130°.
Hence, ∠FAB = 130°.
Answered By
10 Likes
Related Questions
In the given figure, O is the center of the circle, chords AB, CD and EF are equal whereas chords BC, DE and FA are separately equal. The angle AOC is equal to :
80°
100°
90°
120°
In a cyclic-trapezium, the non-parallel sides are equal and the diagonals are also equal. Prove it.
If two sides of a cyclic-quadrilateral are parallel; prove that :
(i) its other two sides are equal.
(ii) its diagonals are equal.
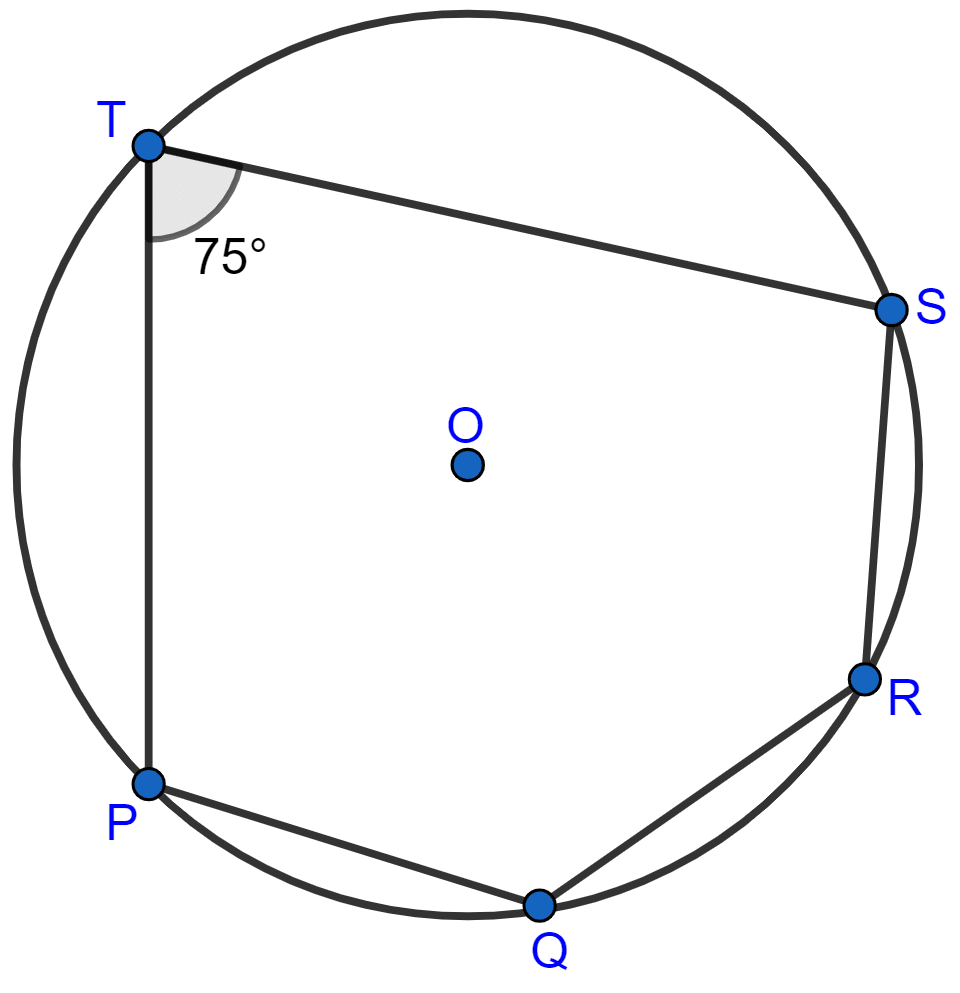
The given figure show a circle with centre O. Also, PQ = QR = RS and ∠PTS = 75°.
Calculate:
(i) ∠POS,
(ii) ∠QOR,
(iii) ∠PQR.