Mathematics
If two sides of a cyclic-quadrilateral are parallel; prove that :
(i) its other two sides are equal.
(ii) its diagonals are equal.
Answer
Let ABCD is a cyclic quadrilateral in which AB || DC. AC and BD are its diagonals.
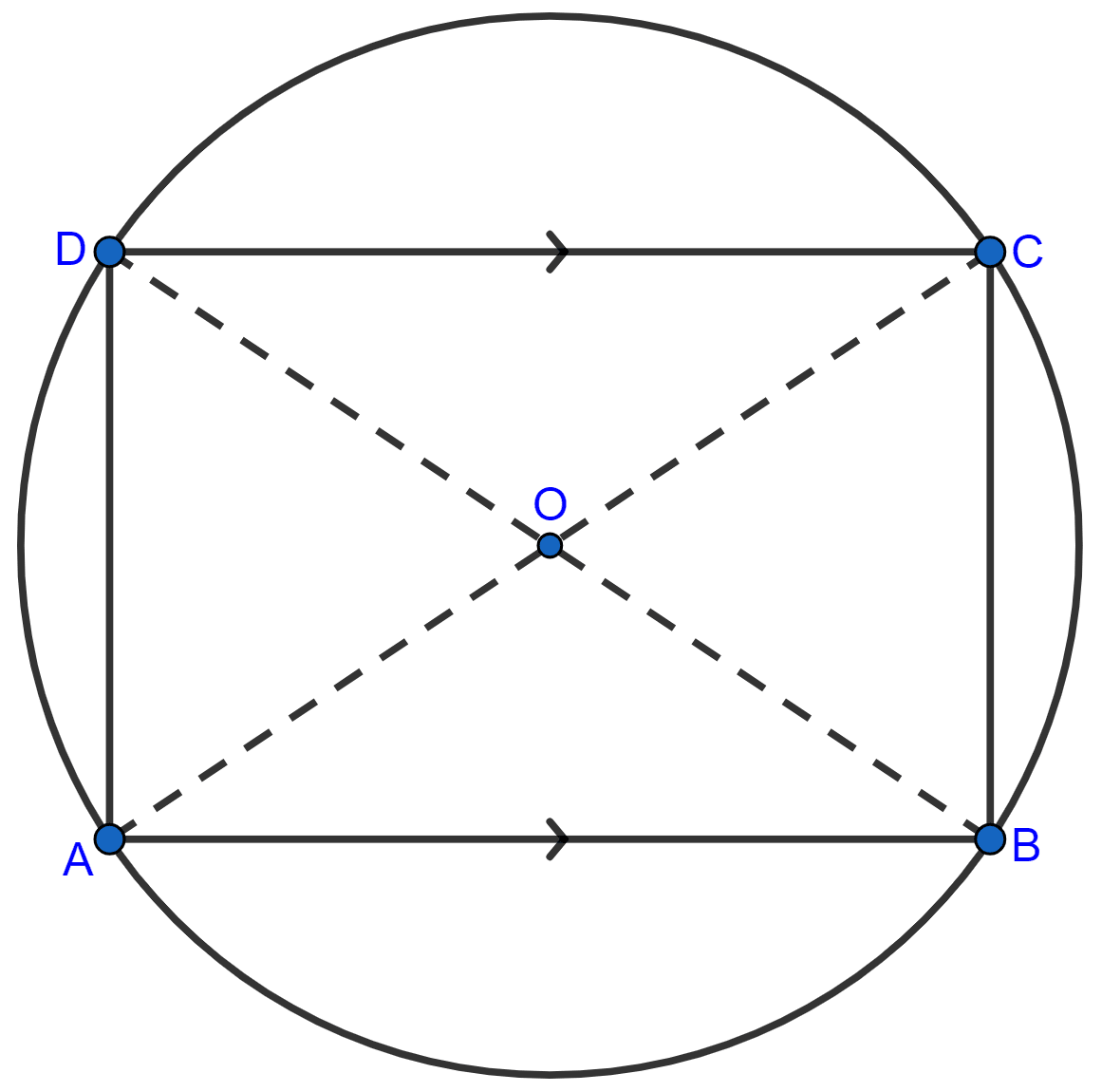
As AB || DC (given)
∠DCA = ∠CAB [Alternate angles are equal]
Chord AD subtends ∠DCA and chord BC subtends ∠CAB at the circumference of the circle.
and
∠DCA = ∠CAB
We know that,
If the angles subtended by 2 chords on the circumference of the circle are equal, then the lengths of the chords are also equal.
∴ chord AD = chord BC or AD = BC.
Hence, proved that AD = BC.
(ii) From figure,
⇒ ∠A + ∠C = 180° [As, sum of opposite angles in a cyclic quadrilateral = 180°]
Also,
⇒ ∠B + ∠C = 180° [Sum of co-interior angles = 180° (As, AB || CD)]
∴ ∠B + ∠C = ∠A + ∠C
⇒ ∠B = ∠A
In ∆ABC and ∆ADB
⇒ AB = AB [Common]
⇒ ∠B = ∠A [Proved above]
⇒ BC = AD [Proved above]
Hence, by SAS criterion of congruence
∆ACB ≅ ∆ADB
∴ AC = BD [By C.P.C.T.]
Hence, proved that AC = BC.
Related Questions
In a cyclic-trapezium, the non-parallel sides are equal and the diagonals are also equal. Prove it.
In the given figure, AB is a side of a regular six-sided polygon and AC is a side of a regular eight-sided polygon inscribed in the circle with centre O. Calculate the sizes of :
(i) ∠AOB,
(ii) ∠ACB,
(iii) ∠ABC.
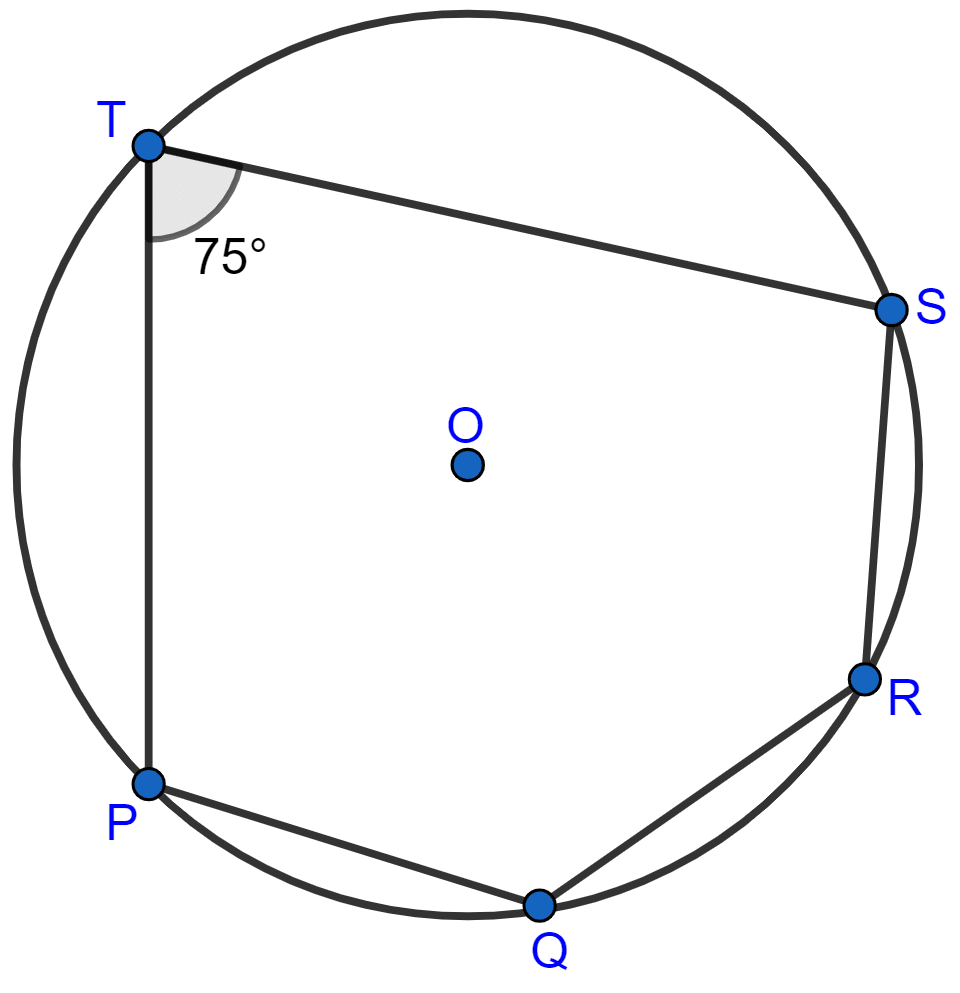
The given figure show a circle with centre O. Also, PQ = QR = RS and ∠PTS = 75°.
Calculate:
(i) ∠POS,
(ii) ∠QOR,
(iii) ∠PQR.
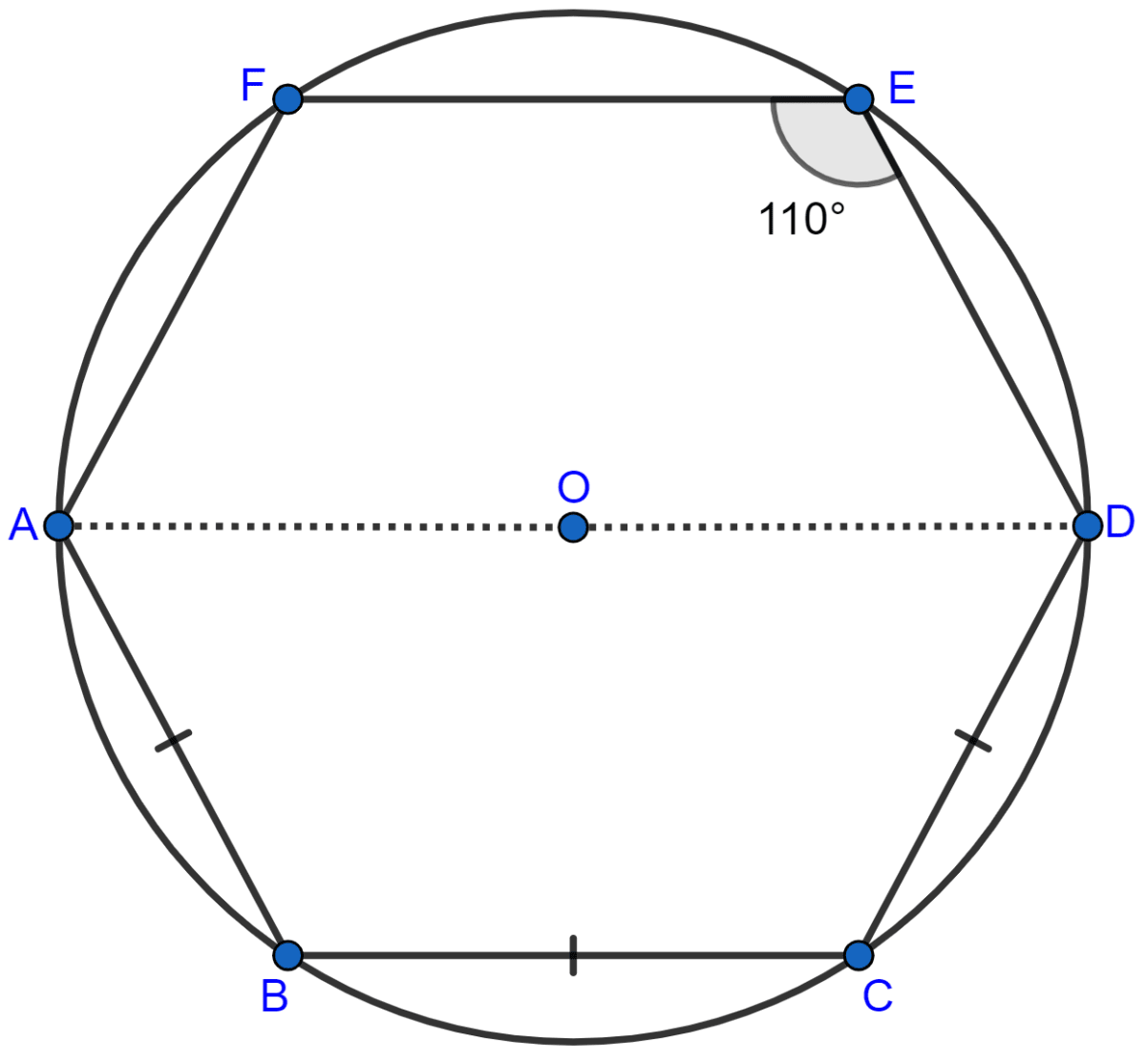
In the following figure, AD is the diameter of the circle with centre O. Chords AB, BC and CD are equal. If ∠DEF = 110°, calculate :
(i) ∠AEF, (ii) ∠FAB.