Mathematics
Find the slope and y-intercept of the following lines :
(i) x - 2y - 1 = 0
(ii) 4x - 5y - 9 = 0
(iii) 3x + 5y + 7 = 0
(iv)
(v) y - 3 = 0
(vi) x - 3 = 0
Straight Line Eq
57 Likes
Answer
(i) The equation of line is
⇒ x - 2y - 1 = 0
⇒ 2y = x - 1
⇒ y =
Comparing the above equation with y = mx + c, we get,
m = and c = .
Hence, the slope of the line = and y-intercept = .
(ii) The equation of line is
⇒ 4x - 5y - 9 = 0
⇒ 5y = 4x - 9
⇒ y =
Comparing the above equation with y = mx + c, we get,
m = and c = .
Hence, the slope of the line = and y-intercept = .
(iii) The equation of line is
⇒ 3x + 5y + 7 = 0
⇒ 5y = -3x - 7
⇒ y =
Comparing the above equation with y = mx + c, we get,
m = and c = .
Hence, the slope of the line = and y-intercept = .
(iv) The equation of line is
Comparing the above equation with y = mx + c, we get,
m = and c = 4.
Hence, the slope of the line = and y-intercept = 4.
(v) The equation of line is
⇒ y - 3 = 0
⇒ y = 3
⇒ y = 0.x + 3
Comparing the above equation with y = mx + c, we get,
m = 0 and c = 3.
Hence, the slope of the line = 0 and y-intercept = 3.
(vi) The equation of line is
⇒ x - 3 = 0
⇒ x = 3.
Here, the slope cannot be defined as the line does not meet y-axis.
Hence, the slope of the line is undefined and there is no y-intercept as line does not meet y-axis.
Answered By
26 Likes
Related Questions
Find the equation of a straight line parallel to y-axis and passing through the point (-3, 5).
Find the equation of a line whose
(i) slope = 3, y-intercept = -5.
(ii) slope = , y-intercept = 3.
(iii) gradient = , y-intercept =
(iv) inclination = 30°, y-intercept = 2.
The equation of the line PQ is 3y - 3x + 7 = 0.
(i) Write down the slope of the line PQ.
(ii) Calculate the angle that the line PQ makes with the positive direction of x-axis.
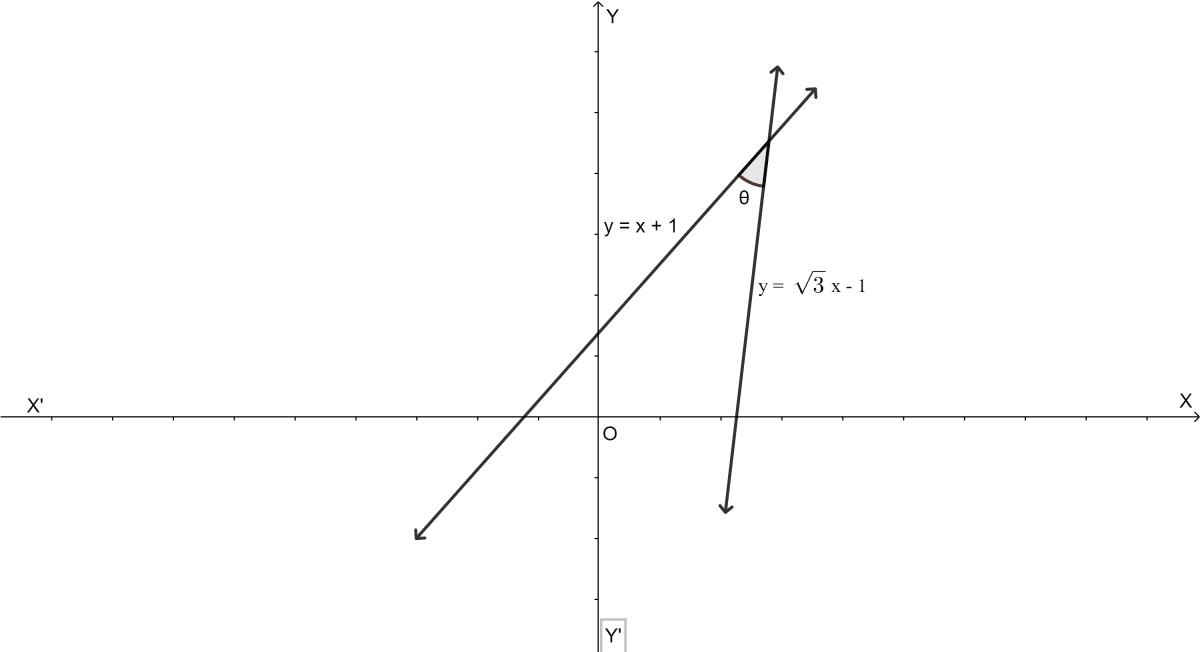
The given figure represents the lines y = x + 1 and y = Write down the angles which the lines make with the positive direction of the x-axis. Hence, determine θ.