Mathematics
Describe the locus of a point P, so that :
AB2 = AP2 + BP2,
where A and B are two fixed points.
Answer
We know that,
Angle subtended by a diameter on any point of a circle is 90°.
From figure,
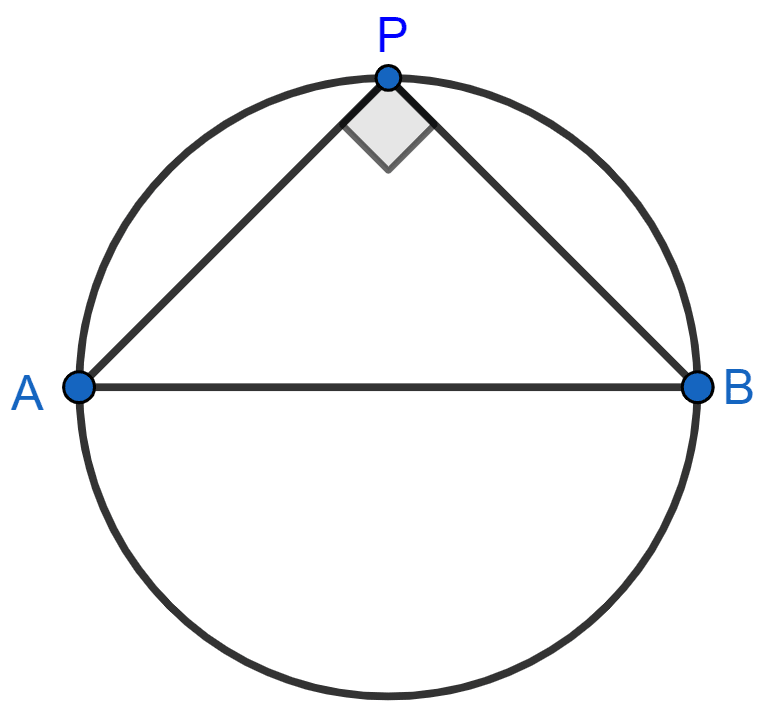
By pythagoras theorem,
⇒ Hypotenuse2 = Perpendicular2 + Base2
⇒ AB2 = AP2 + BP2
We know that,
Pythagoras theorem applies on right angle triangle.
∴ AP ⊥ BP.
Hence, the locus of the point P is the circumference of a circle with AB as diameter.
Related Questions
Describe :
(i) The locus of points at distances less than 3 cm from a given point.
(ii) The locus of points at distances greater than 4 cm from a given point.
(iii) The locus of points at distances less than or equal to 2.5 cm from a given point.
(iv) The locus of points at distances greater than or equal to 35 mm from a given point.
(v) The locus of the center of a given circle which rolls around the outside of a second circle and is always touching it.
(vi) The locus of the centers of all circles that are tangent to both the arms of a given angle.
(vii) The locus of the mid-points of all chords parallel to a given chord of a circle.
(viii) The locus of points within a circle that are equidistant from the end points of a given chord.
Describe the locus of vertices of all isosceles triangles having a common base.
Describe the locus of the centers of all circles passing through two fixed points.
Describe the locus of a point in rhombus ABCD, so that it is equidistant from
(i) AB and BC.
(ii) B and D.