Mathematics
Any point D is taken on the side BC of a ∆ABC and AD is produced to E such that AD = DE, prove that area of ∆BCE = area of ∆ABC.
Answer
∆ABC with point D on the side BC and AD produced to E such that AD = DE is shown below:
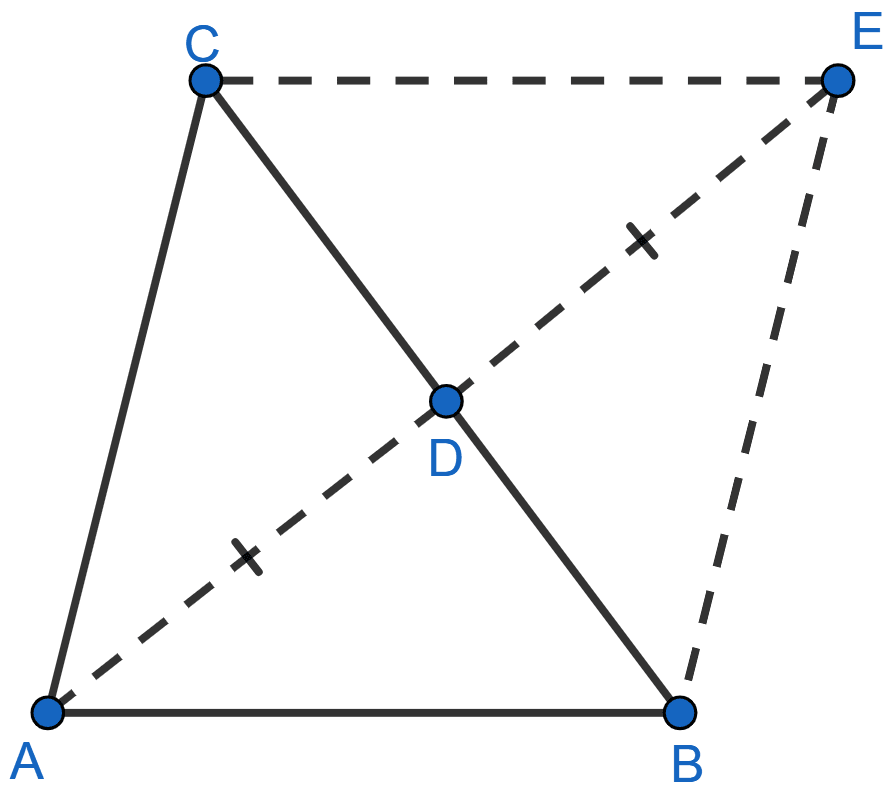
In ∆ABE, it is given that AD = DE.
∴ BD is the median of ∆ABE
⇒ area of ∆ABD = area of ∆BED …….. (i)
Similarly,
In ∆ACE, it is given that AD = AE
∴ CD is the median of ∆ACE
⇒ area of ∆ACD = area of ∆CED …….. (ii)
By adding (i) and (ii), we get
⇒ area of ∆ABD + area of ∆ACD = area of ∆BED + area of ∆CED
⇒ area of ∆ABC = area of ∆BCE.
Hence, proved that area of ∆ABC = area of ∆BCE.
Related Questions
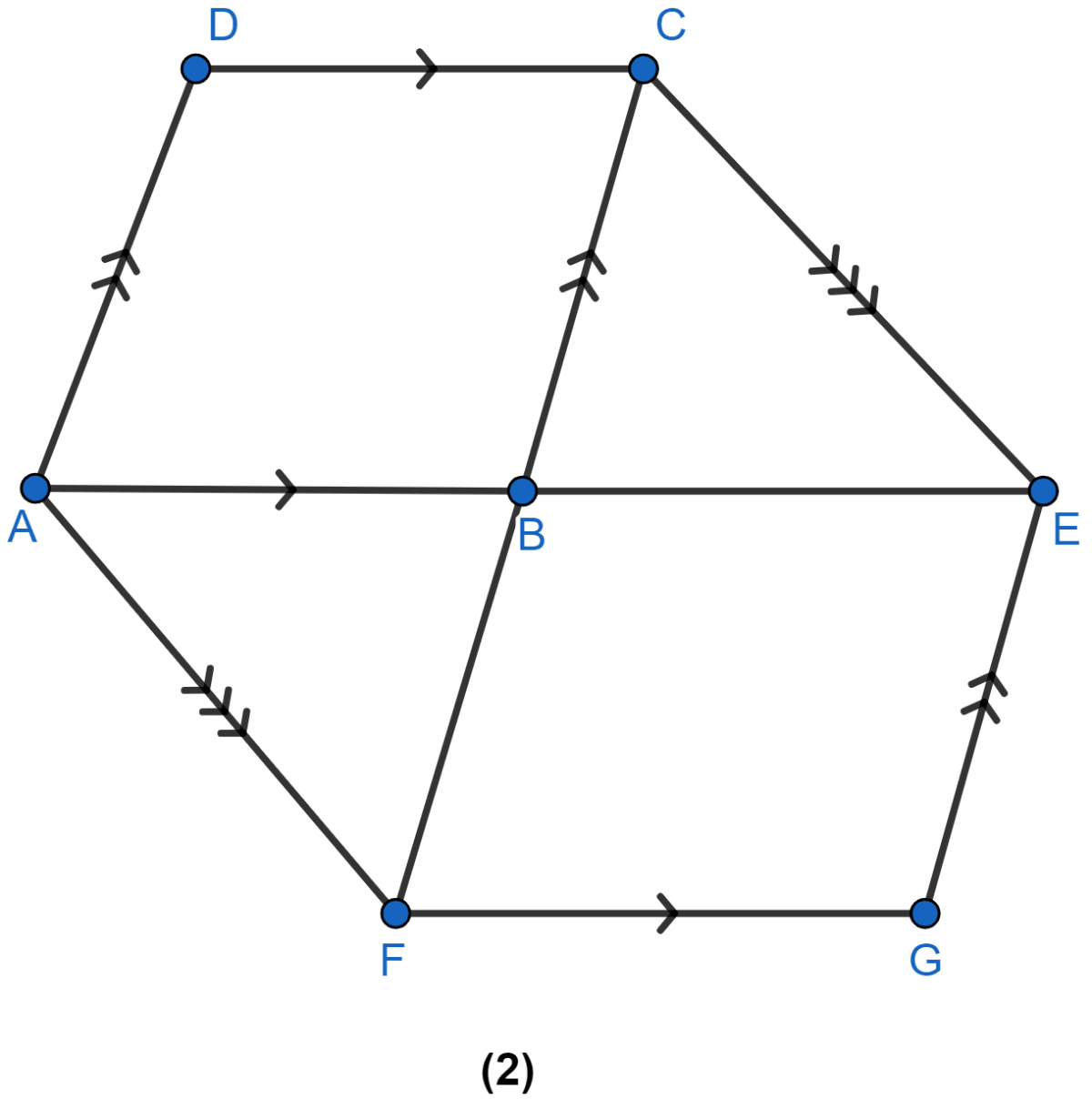
In figure (2) given below, the side AB of the parallelogram ABCD is produced to E. A straight line through A is drawn parallel to CE to meet CB produced at F and parallelogram BFGE is completed. Prove that
area of || gm BFGE = area of || gm ABCD.
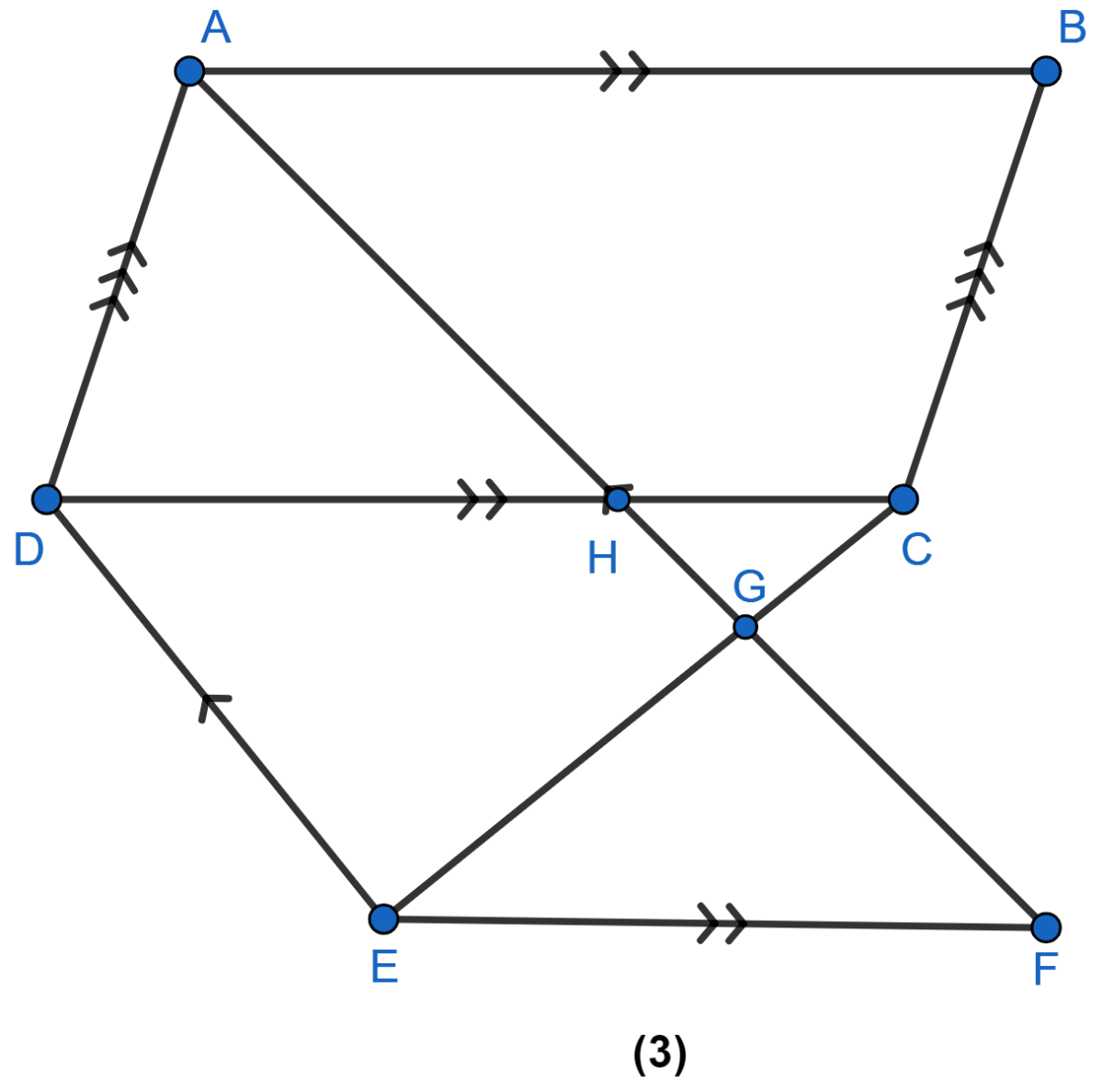
In figure (3) given below, AB || DC || EF, AD || BE and DE || AF. Prove that the area of DEFH is equal to the area of ABCD.
ABCD is a rectangle and P is the mid-point of AB. DP is produced to meet CB at Q. Prove that the area of rectangle ABCD = area of ∆DQC.
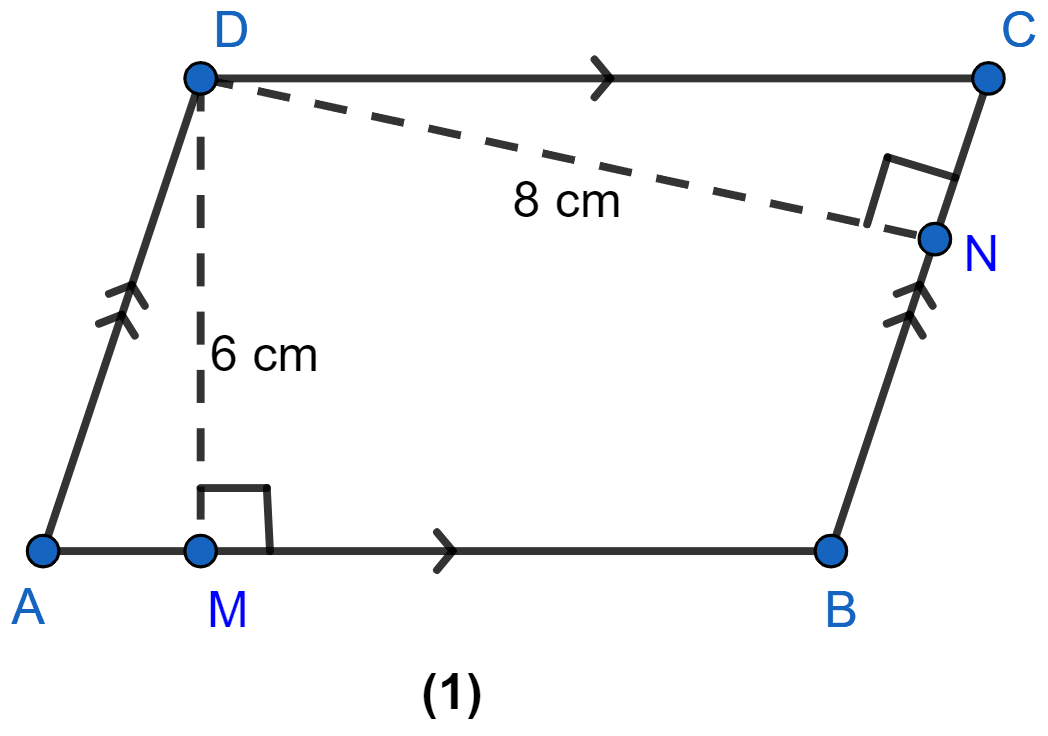
In figure (1) given below, the perimeter of the parallelogram is 42 cm. Calculate the lengths of the sides of the parallelogram.