Mathematics
An aeroplane at an altitude of 250 m observes the angle of depression of two boats on the opposite banks of a river to be 45° and 60° respectively. Find the width of the river. Write the answer correct to the nearest whole number.
Heights & Distances
96 Likes
Answer
Let aeroplane be at point D and boats be at point A and B. Since, aeroplane is at an altitude of 250 m therefore,
∴ CD = 250 m.
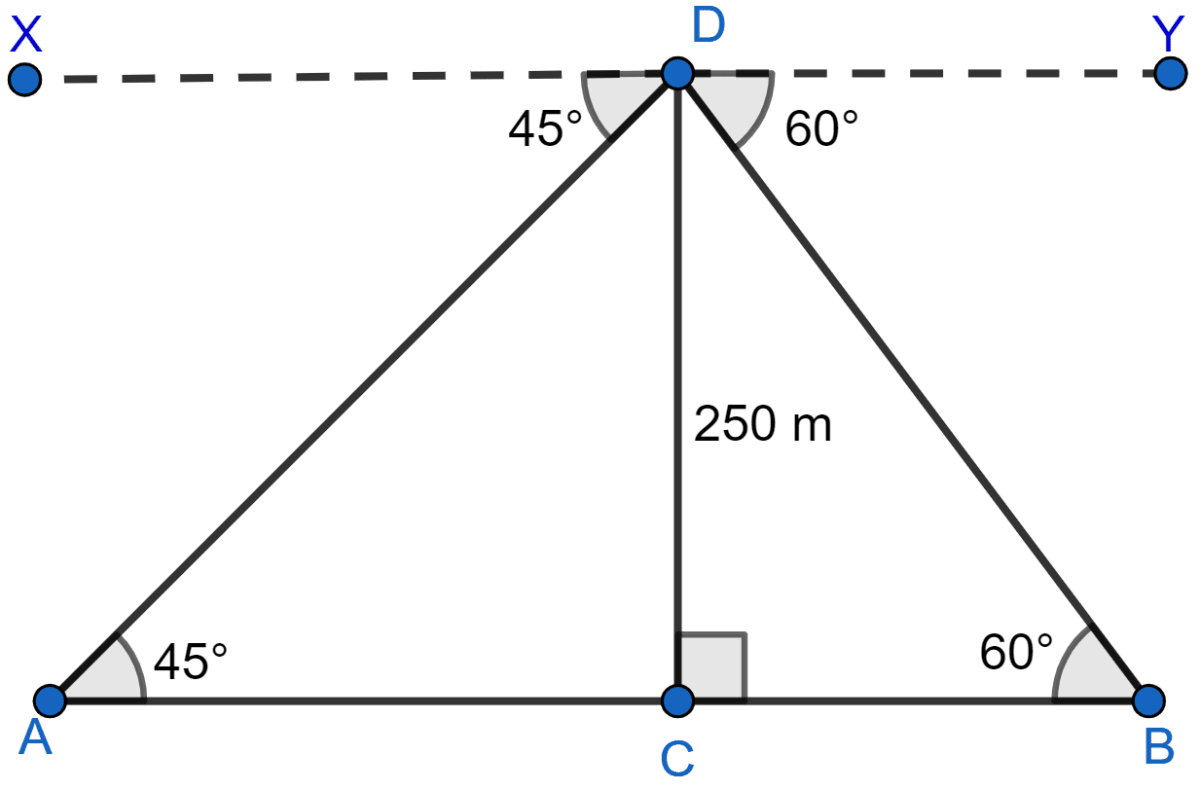
From figure,
∠DAC = ∠XDA = 45° (Alternate angles are equal)
∠DBC = ∠YDB = 60° (Alternate angles are equal)
Considering right angled △BCD, we get
Considering right angled △ACD, we get
Width of the river (AB) = AC + BC = 144.34 + 250 = 394.34 meters.
Rounding off to nearest meter AB = 394 meters.
Hence, the width of the river is 394 meters.
Answered By
33 Likes
Related Questions
From two points A and B on the same side of a building, the angles of elevation of the top of the building are 30° and 60° respectively. If the height of the building is 10 m, find the distance between A and B correct to two decimal places.
The angles of depression of two ships A and B as observed from the top of a light house 60 m high are 60° and 45° respectively. If the two ships are on the opposite sides of the light house, find the distance between the two ships. Give your answer correct to the nearest whole number.
From a tower 126 m high, the angles of depression of two rocks which are in a horizontal line through the base of the tower are 16° and 12° 20'. Find the distance between the rocks if they are on
(i) the same side of the tower
(ii) the opposite sides of the tower.
A man 1.8 m high stands at a distance of 3.6 m from a lamp post and casts a shadow of 5.4 m on the ground. Find the height of the lamp post.