Mathematics
From a tower 126 m high, the angles of depression of two rocks which are in a horizontal line through the base of the tower are 16° and 12° 20'. Find the distance between the rocks if they are on
(i) the same side of the tower
(ii) the opposite sides of the tower.
Heights & Distances
89 Likes
Answer
(i) Let the rocks be at point A and D.
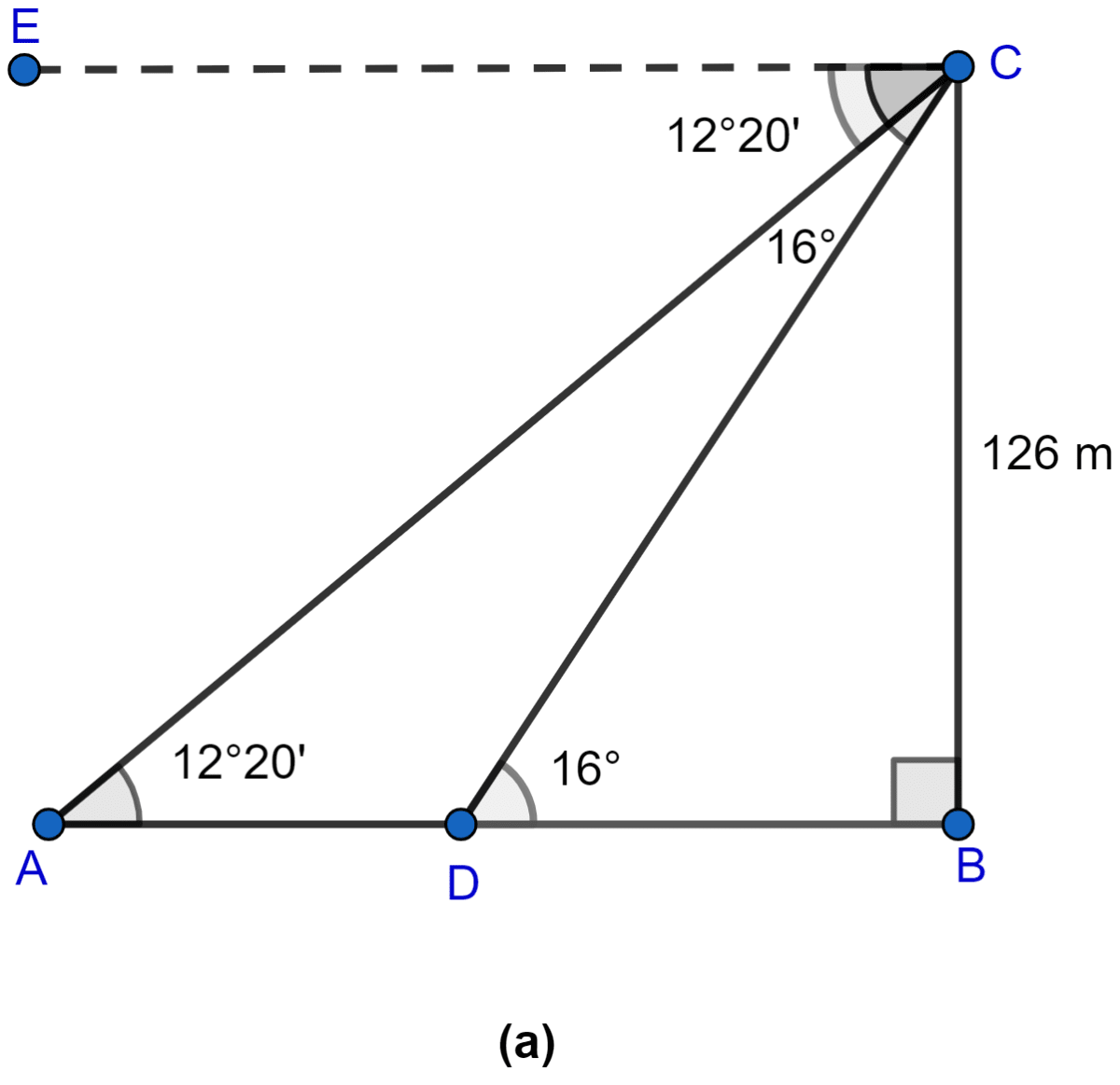
From figure a,
∠CAB = ∠ECA = 12° 20' (Alternate angles are equal)
∠CDB = ∠ECD = 16° (Alternate angles are equal)
Considering right angled △ABC, we get
Considering right angled △BCD, we get
Distance between two rocks (AD) = AB - BD = 576.29 - 439.48 = 136.81
Hence, the distance between two rocks when they are on same side of the tower is 136.81 meters.
(ii) Let the rocks be at point A and B.
From figure b,
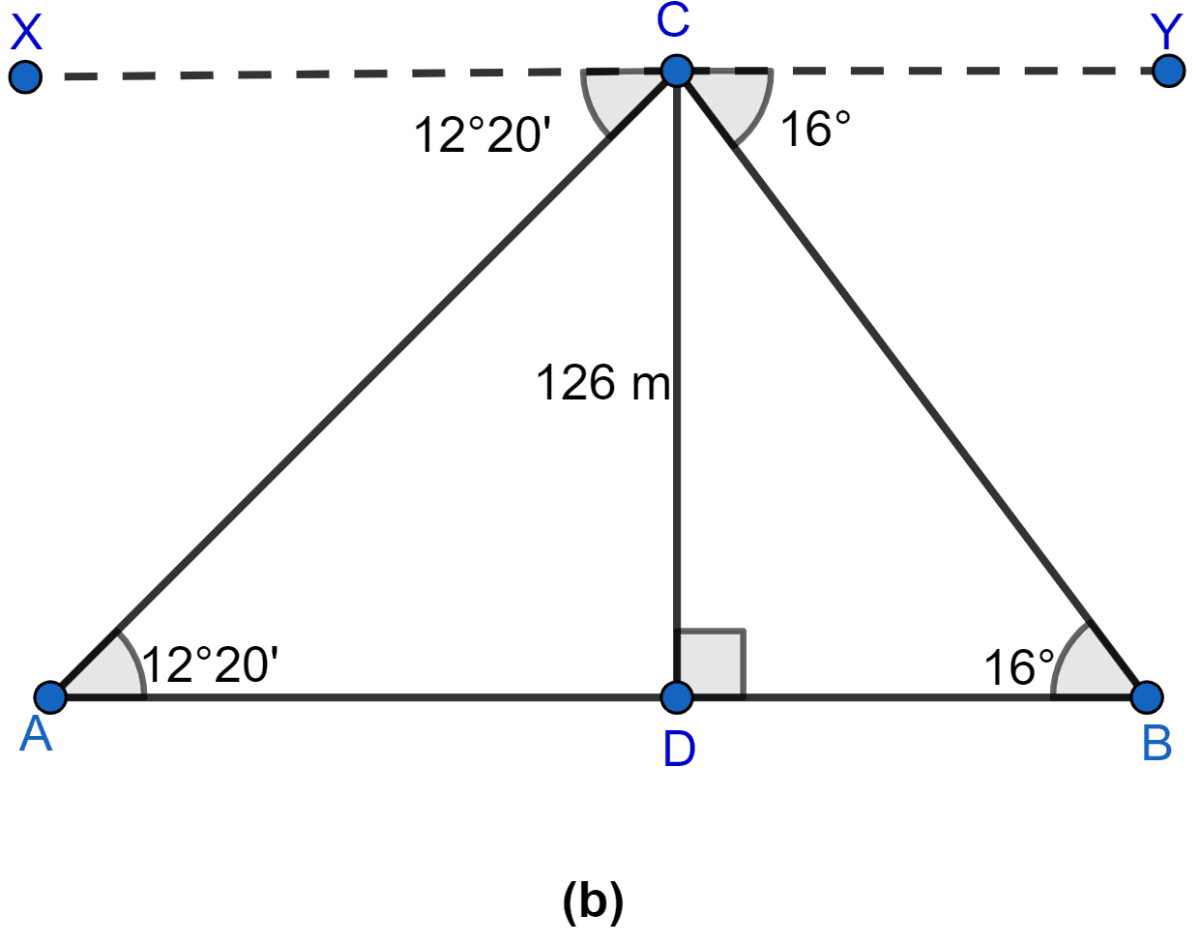
∠CAD = ∠XCA = 12° 20' (Alternate angles are equal)
∠CBD = ∠YCB = 16° (Alternate angles are equal)
Considering right angled △ADC, we get
Considering right angled △BCD, we get
Distance between two rocks (AB) = AD + DB = 576.29 + 439.48 = 1015.7
Hence, the distance between two rocks when they are on opposite sides of the tower is 1015.7 meters.
Answered By
25 Likes
Related Questions
The angles of depression of two ships A and B as observed from the top of a light house 60 m high are 60° and 45° respectively. If the two ships are on the opposite sides of the light house, find the distance between the two ships. Give your answer correct to the nearest whole number.
An aeroplane at an altitude of 250 m observes the angle of depression of two boats on the opposite banks of a river to be 45° and 60° respectively. Find the width of the river. Write the answer correct to the nearest whole number.
A man 1.8 m high stands at a distance of 3.6 m from a lamp post and casts a shadow of 5.4 m on the ground. Find the height of the lamp post.
The angles of depression of the top and the bottom of a 8 m tall building from the top of a multi-storeyed building are 30° and 45° respectively. Find the height of the multi storeyed building and the distance between the two buildings, correct to two decimal places.