Mathematics
ABCD is a square. E, F, G and H are points on the sides AB, BC, CD and DA respectively such that AE = BF = CG = DH. Prove that EFGH is a square.
Answer
Given, AE = BF = CG = DH
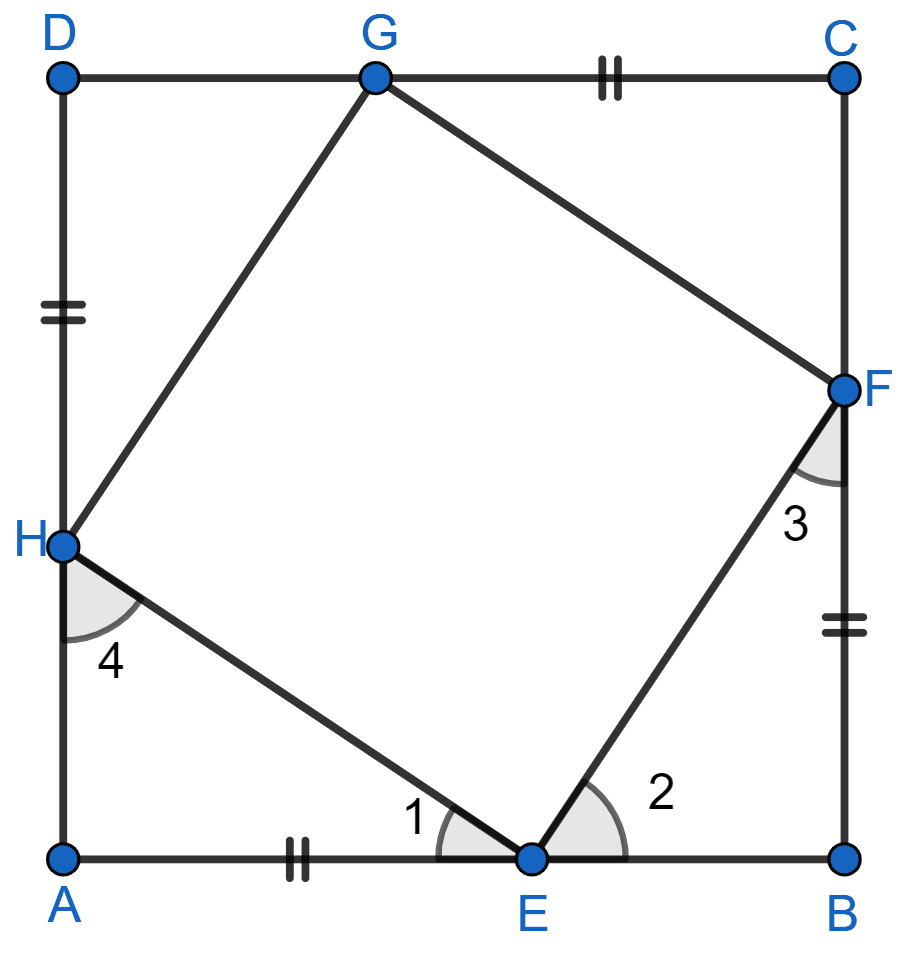
Since, ABCD is a square and AB = BC = CD = AD.
So,
⇒ AB - AE = BC - BF = CD - CG = AD - DH
⇒ EB = FC = GD = AH
Now, in ∆AEH and ∆BFE
⇒ AE = BF [Given]
⇒ AH = EB [Proved]
⇒ ∠A = ∠B [Each 90°]
So, ∆AEH ≅ ∆BFE by S.A.S axiom of congruency
Then, by C.P.C.T we have
⇒ EH = EF and ∠4 = ∠2
In ∆AEH,
⇒ ∠1 + ∠4 + ∠HAE = 180°
⇒ ∠1 + ∠4 + 90° = 180°
⇒ ∠1 + ∠4 = 90°
⇒ ∠1 + ∠2 = 90° [Since, ∠4 = ∠2]
From figure,
⇒ ∠1 + ∠HEF + ∠2 = 180°
⇒ ∠HEF + 90° = 180°
⇒ ∠HEF = ∠E = 90°.
In ∆DGH and ∆CGF
⇒ DH = GC [Given]
⇒ GD = FC [Proved]
⇒ ∠D = ∠C [Each 90°]
So, ∆DGH ≅ ∆CGF by S.A.S axiom of congruency
Then, by C.P.C.T we have
GH = FG
In ∆DGH and ∆AEH
⇒ DH = AE [Given]
⇒ GD = HA [Proved]
⇒ ∠D = ∠A [Each 90°]
So, ∆DGH ≅ ∆AEH by S.A.S axiom of congruency
Then, by C.P.C.T we have
GH = HE
Thus, EF = FG = GH = HE, therefore EFGH is a Rhombus.
∵ One angle of rhombus EFGH is 90° (∠HEF = 90°),
∴ EFGH is a square.
Hence, proved that EFGH is a square.
Related Questions
ABCD is a parallelogram, bisectors of angles A and B meet at E which lies on DC. Prove that AB = 2AD.
ABCD is a square and the diagonals intersect at O. If P is a point on AB such that AO = AP, prove that 3∠POB = ∠AOP.
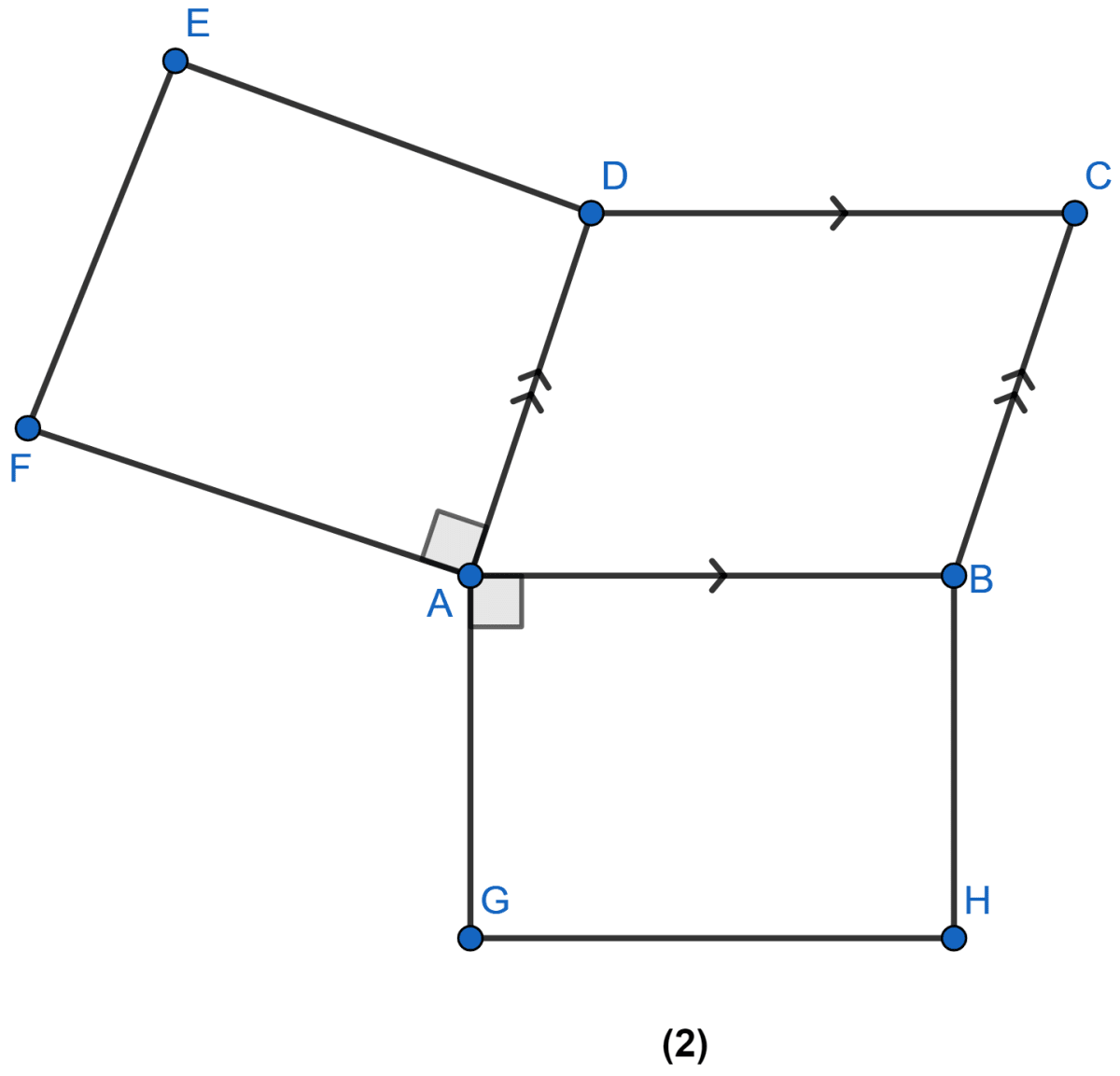
In the figure (1) given below, ABCD and ABEF are parallelograms. Prove that
(i) CDFE is a parallelogram.
(ii) FD = EC
(iii) △AFD ≅ △BEC.
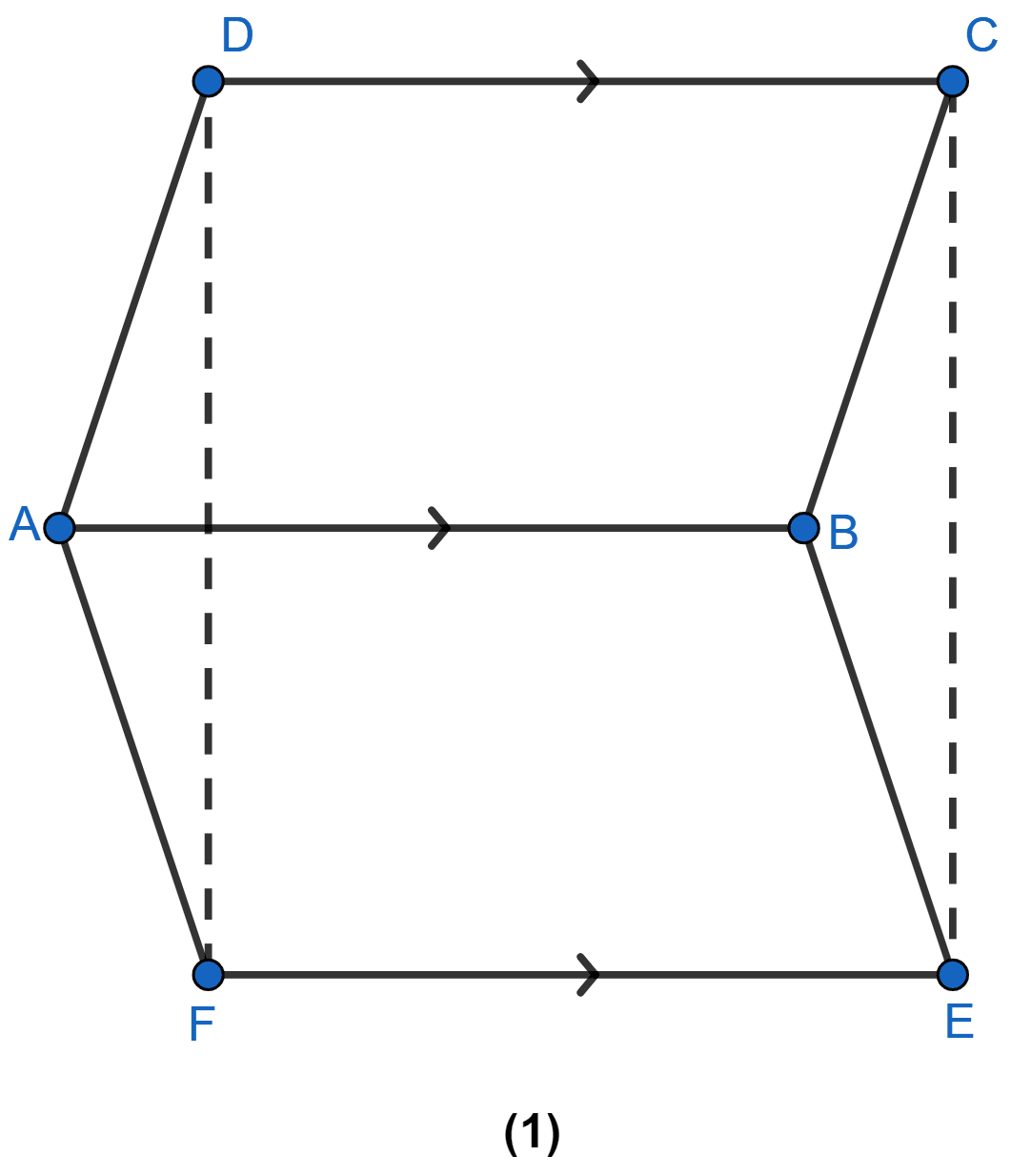
In the figure (2) given below, ABCD is a parallelogram, ADEF and AGHB are two squares. Prove that FG = AC.