Mathematics
ABCD is a square and the diagonals intersect at O. If P is a point on AB such that AO = AP, prove that 3∠POB = ∠AOP.
Rectilinear Figures
40 Likes
Answer
In square ABCD, AC is a diagonal.

So, ∠CAB = 45° (As diagonals bisect vertex angle)
∠OAP = 45°
In ∆AOP,
∠OAP = 45°
AO = AP [Given]
∠AOP = ∠APO = x (let) [Angles opposite to equal sides are equal]
Now,
∠AOP + ∠APO + ∠OAP = 180° [Angles sum property of a triangle]
∠AOP + ∠AOP + 45° = 180°
2x = 180° – 45°
x =
∠AOB = 90° [Diagonals of a square bisect at right angles]
So, ∠AOP + ∠POB = 90°
+ ∠POB = 90°
∠POB = 90° –
=
3∠POB = = ∠AOP.
Hence, proved that 3∠POB = ∠AOP.
Answered By
31 Likes
Related Questions
In parallelogram ABCD, the bisector of ∠A meets DC in E and AB = 2AD. Prove that
(i) BE bisects ∠B
(ii) ∠AEB = a right angle.
ABCD is a parallelogram, bisectors of angles A and B meet at E which lies on DC. Prove that AB = 2AD.
ABCD is a square. E, F, G and H are points on the sides AB, BC, CD and DA respectively such that AE = BF = CG = DH. Prove that EFGH is a square.
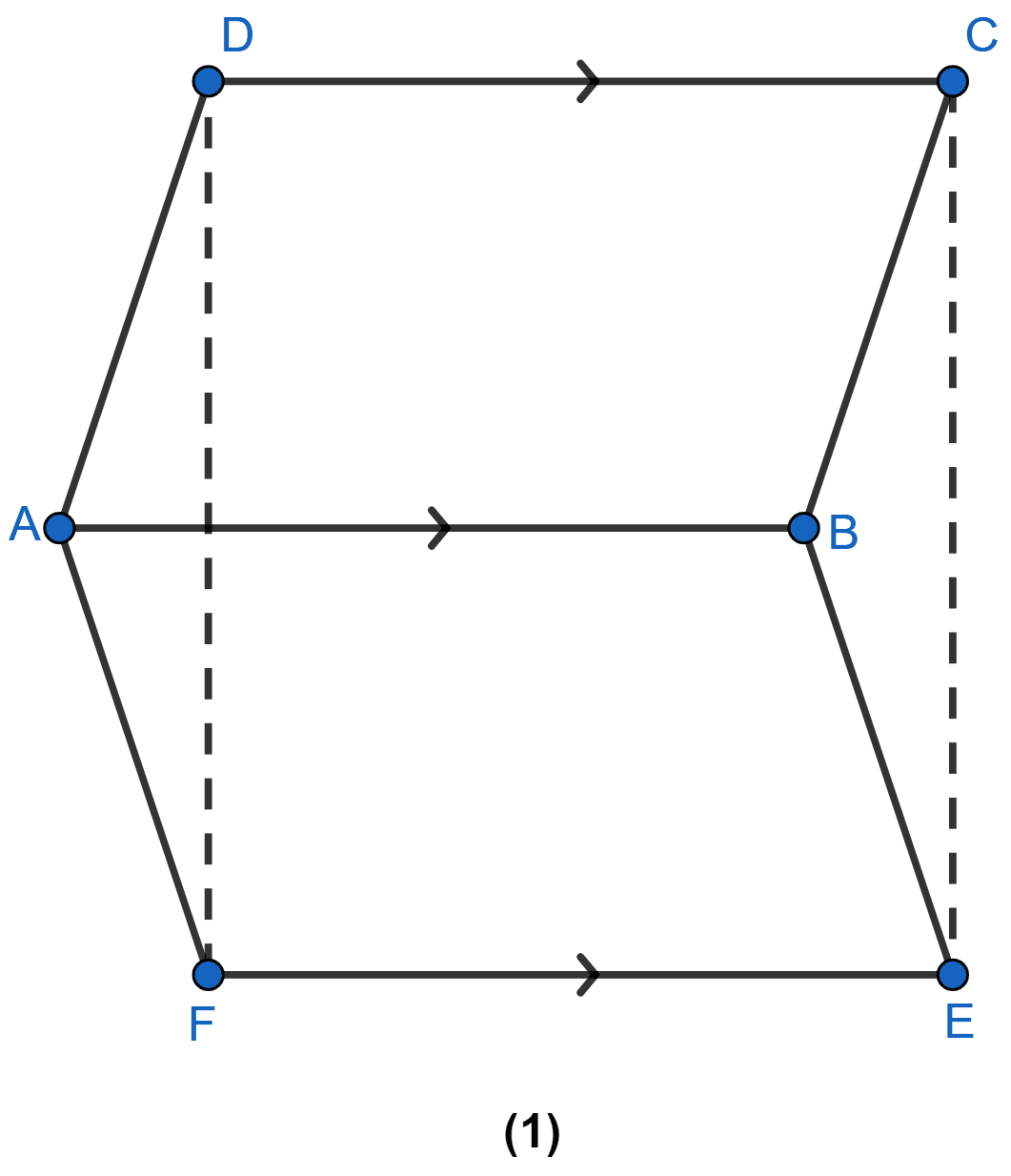
In the figure (1) given below, ABCD and ABEF are parallelograms. Prove that
(i) CDFE is a parallelogram.
(ii) FD = EC
(iii) △AFD ≅ △BEC.