Mathematics
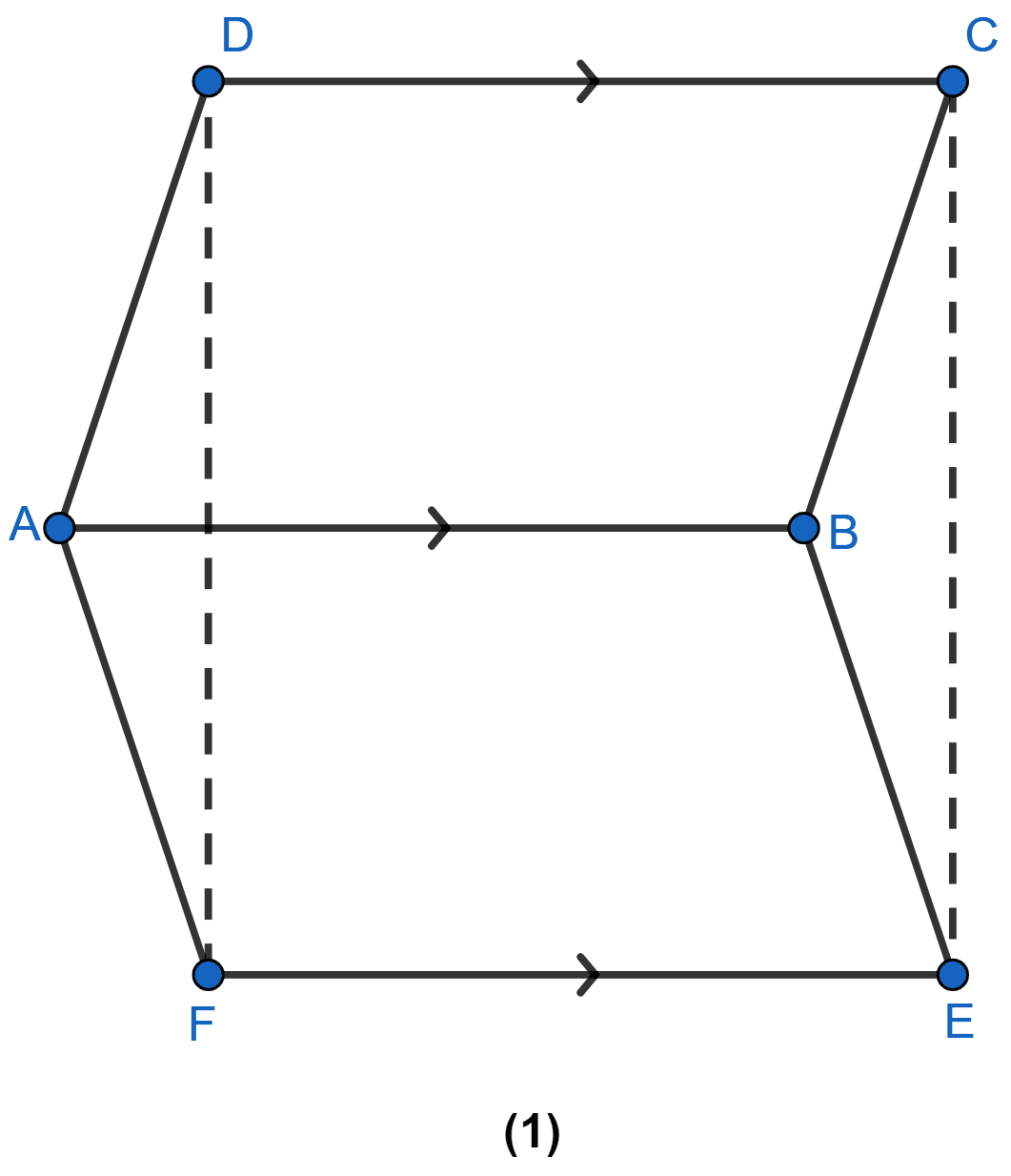
In the figure (1) given below, ABCD and ABEF are parallelograms. Prove that
(i) CDFE is a parallelogram.
(ii) FD = EC
(iii) △AFD ≅ △BEC.
Rectilinear Figures
26 Likes
Answer
(i) DC || AB and DC = AB [∵ ABCD is a || gm] ………. (1)
FE || AB and FE = AB [∵ ABEF is a || gm] ………..(2)
∴ DC || FE and DC = FE [From (1) and (2)]
Hence, proved that CDFE is a || gm.
(ii) Since, CDEF is a || gm.
So, FD = EC (As opposite sides of a || gm are equal)
Hence, proved that FD = EC.
(iii) In ∆AFD and ∆BEC, we have
AD = BC [Opposite sides of || gm ABCD are equal]
AF = BE [Opposite sides of || gm ABEF are equal]
FD = CE [Opposite sides of || gm CDFE are equal]
Hence, ∆AFD ≅ ∆BEC by S.S.S axiom of congruency
Hence, proved that ∆AFD ≅ ∆BEC.
Answered By
19 Likes
Related Questions
ABCD is a square and the diagonals intersect at O. If P is a point on AB such that AO = AP, prove that 3∠POB = ∠AOP.
ABCD is a square. E, F, G and H are points on the sides AB, BC, CD and DA respectively such that AE = BF = CG = DH. Prove that EFGH is a square.
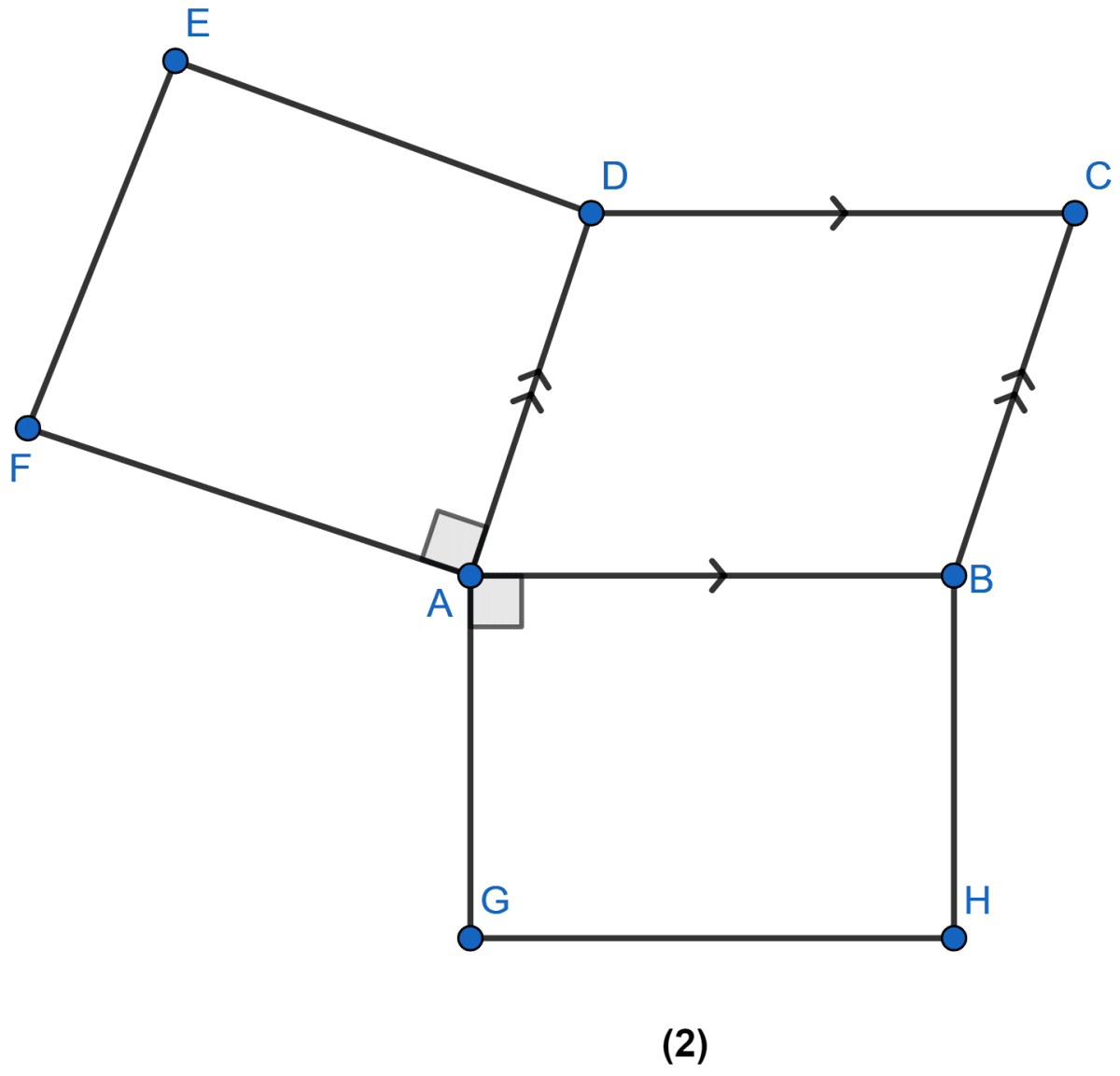
In the figure (2) given below, ABCD is a parallelogram, ADEF and AGHB are two squares. Prove that FG = AC.
ABCD is a rhombus in which ∠A = 60°. Find the ratio AC : BD.