Mathematics
ABCD is a rhombus in which ∠A = 60°. Find the ratio AC : BD.
Rectilinear Figures
32 Likes
Answer
Rhombus ABCD is shown in the figure below:
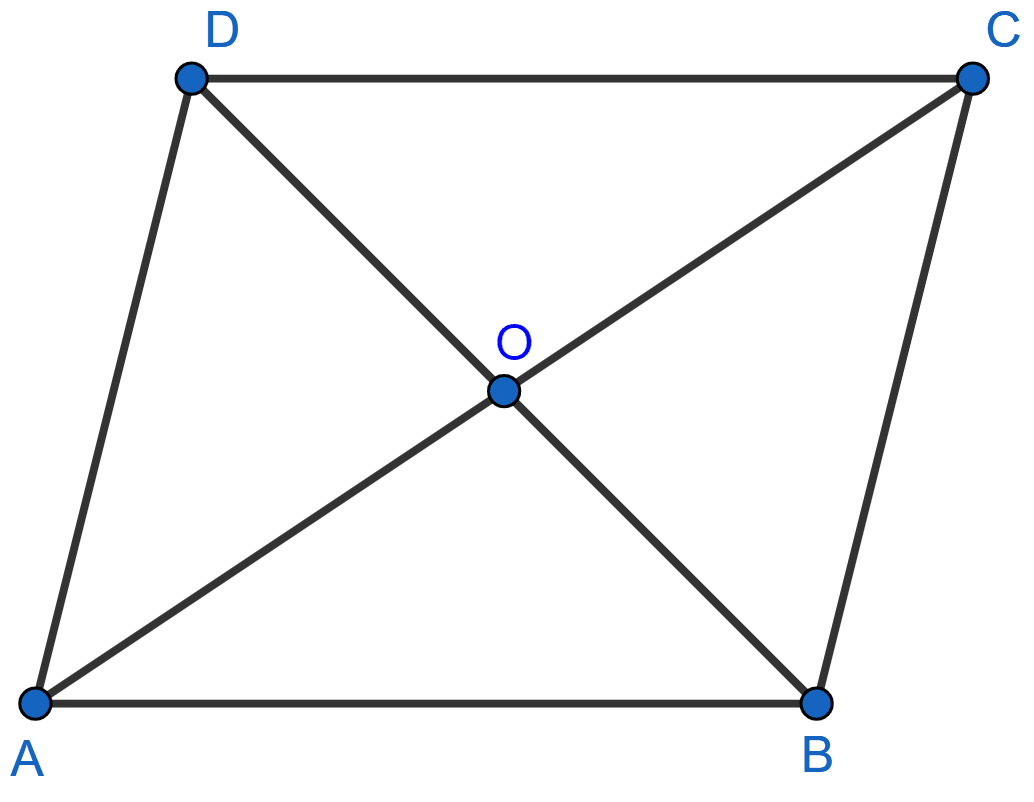
In △ABD,
⇒ AB = AD (Sides of rhombus are equal.)
⇒ ∠B = ∠D = x (let) (∵ angles opposite to equal sides are equal)
⇒ ∠A + ∠B + ∠D = 180°
⇒ 60° + x + x = 180°
⇒ 2x = 180° - 60°
⇒ 2x = 120°
⇒ x = 60°.
∴ ABD is an equilateral triangle.
So, BD = AB = AD = a (let)
Since, diagonals of rhombus bisect each other,
OB =
In right angled triangle AOB,
AB2 = AO2 + OB2
a2 = AO2 +
AO2 = a2 -
AO =
AC = 2AO =
AC : BD = .
Hence, AC : BD = .
Answered By
24 Likes
Related Questions
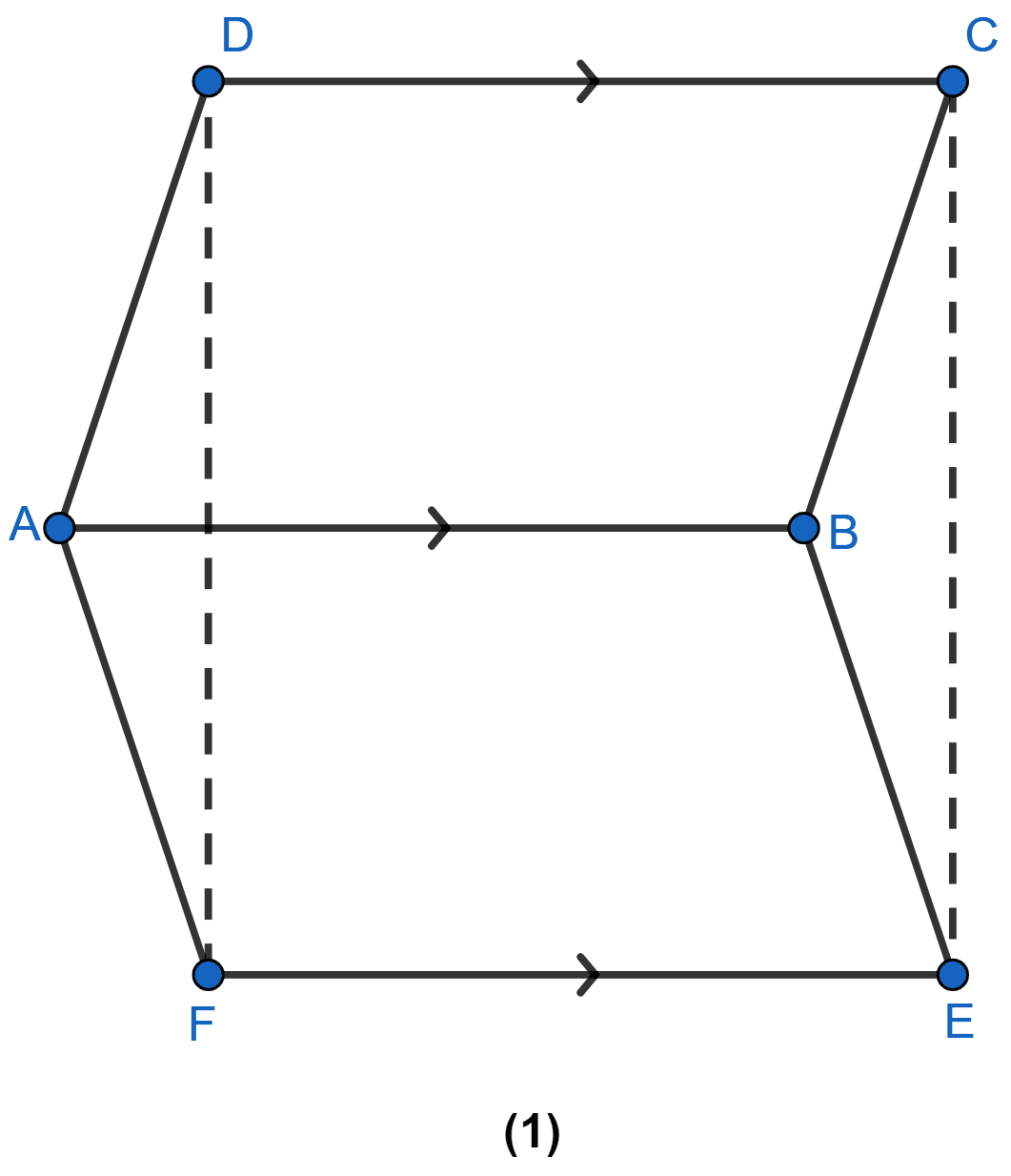
In the figure (1) given below, ABCD and ABEF are parallelograms. Prove that
(i) CDFE is a parallelogram.
(ii) FD = EC
(iii) △AFD ≅ △BEC.
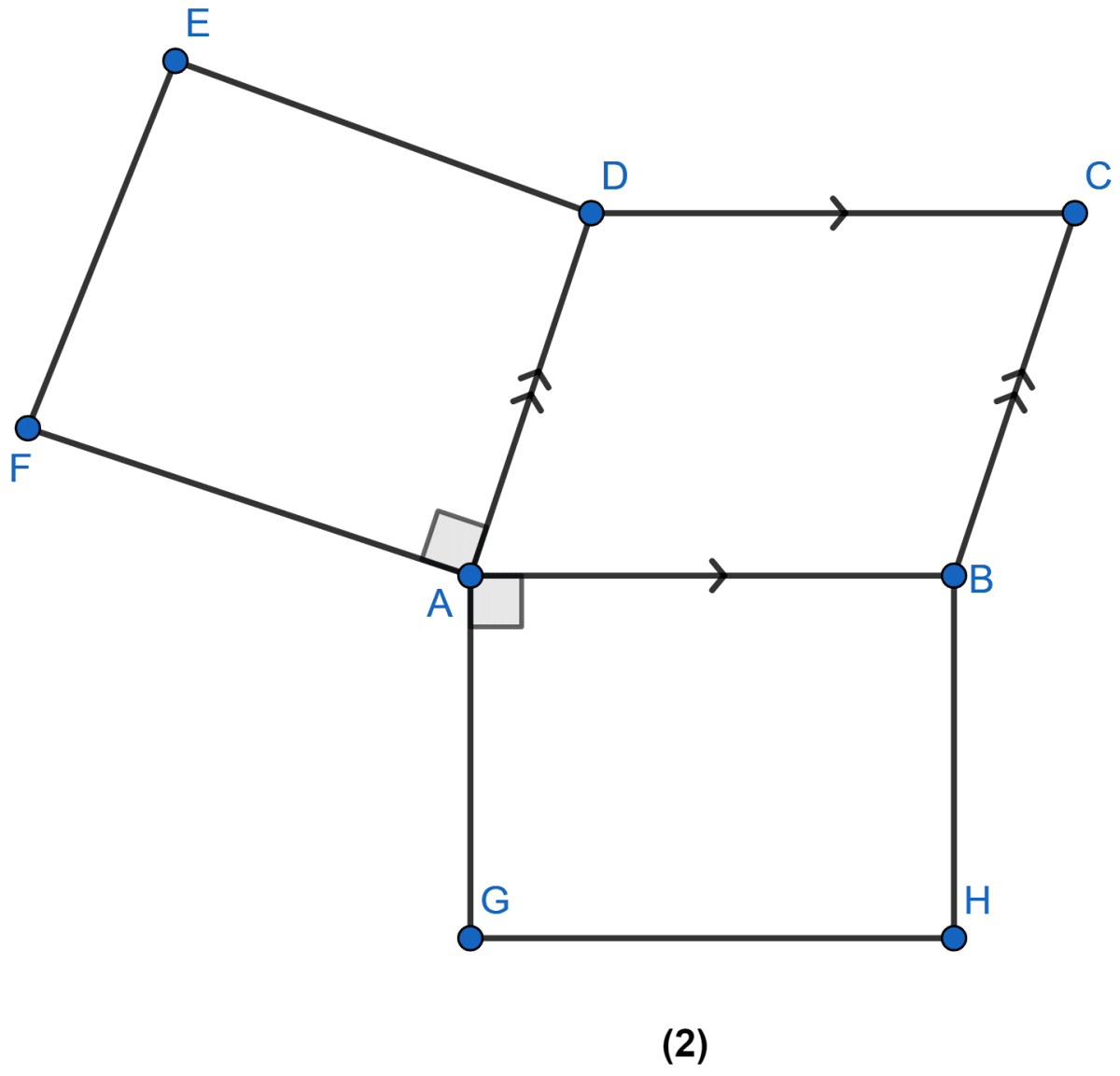
In the figure (2) given below, ABCD is a parallelogram, ADEF and AGHB are two squares. Prove that FG = AC.
Using ruler and compasses only, construct the quadrilateral ABCD in which ∠BAD = 45°, AD = AB = 6cm, BC = 3.6cm, CD = 5cm. Measure ∠BCD.
Draw a quadrilateral ABCD with AB = 6 cm, BC = 4 cm, CD = 4 cm and ∠ABC = ∠BCD = 90°.