Mathematics
ABCD is a square and the diagonals intersect at O. If P is a point on AB such that AO = AP, prove that 3∠POB = ∠AOP.
Related Questions
In parallelogram ABCD, the bisector of ∠A meets DC in E and AB = 2AD. Prove that
(i) BE bisects ∠B
(ii) ∠AEB = a right angle.
ABCD is a parallelogram, bisectors of angles A and B meet at E which lies on DC. Prove that AB = 2AD.
ABCD is a square. E, F, G and H are points on the sides AB, BC, CD and DA respectively such that AE = BF = CG = DH. Prove that EFGH is a square.
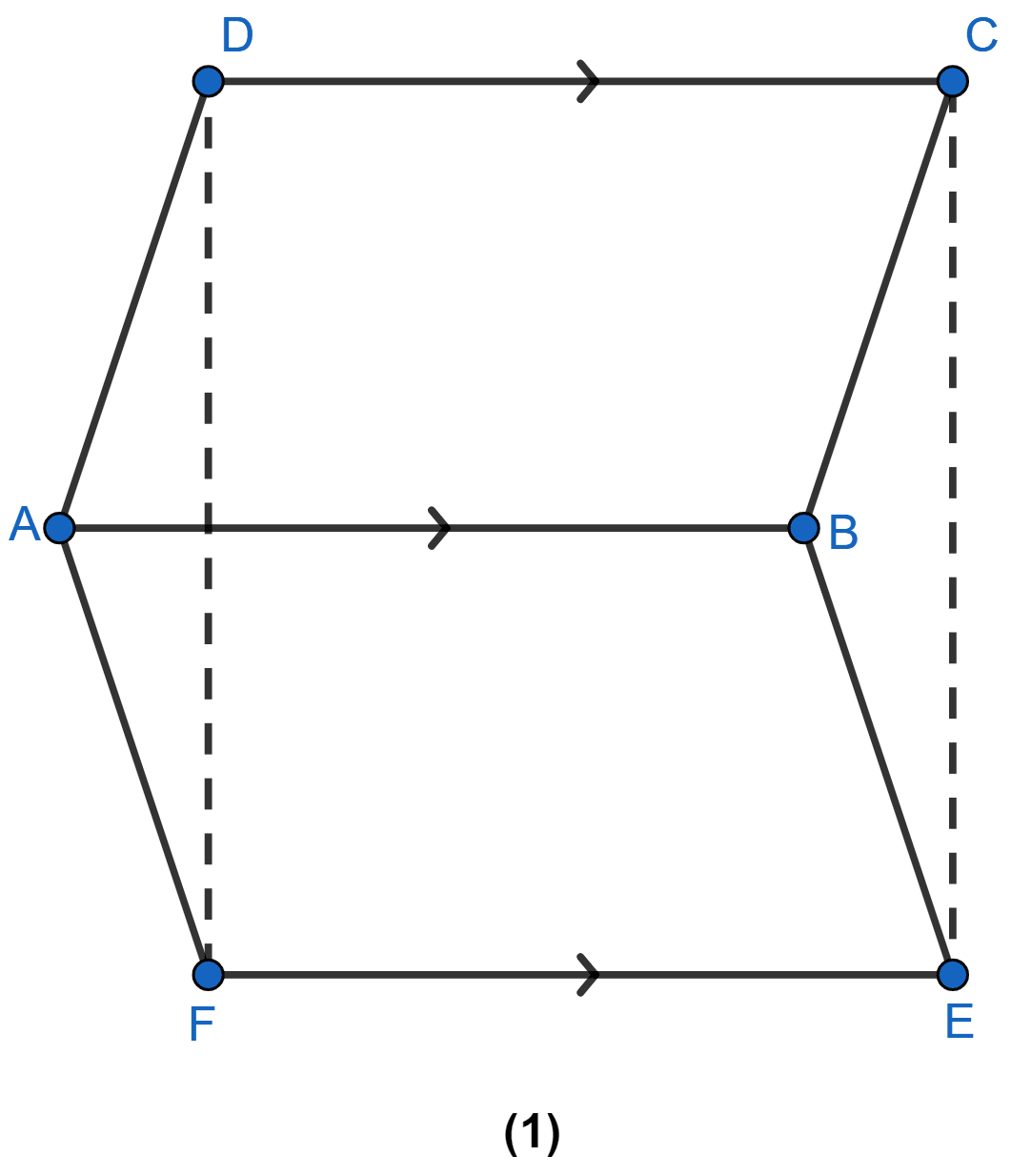
In the figure (1) given below, ABCD and ABEF are parallelograms. Prove that
(i) CDFE is a parallelogram.
(ii) FD = EC
(iii) △AFD ≅ △BEC.