Mathematics
ABCD is a cyclic quadrilateral such that AB is a diameter of the circle circumscribing it and ∠ADC = 140°, then ∠BAC is equal to
80°
50°
40°
30°
Answer
Cyclic quadrilateral ABCD is shown in the figure below:
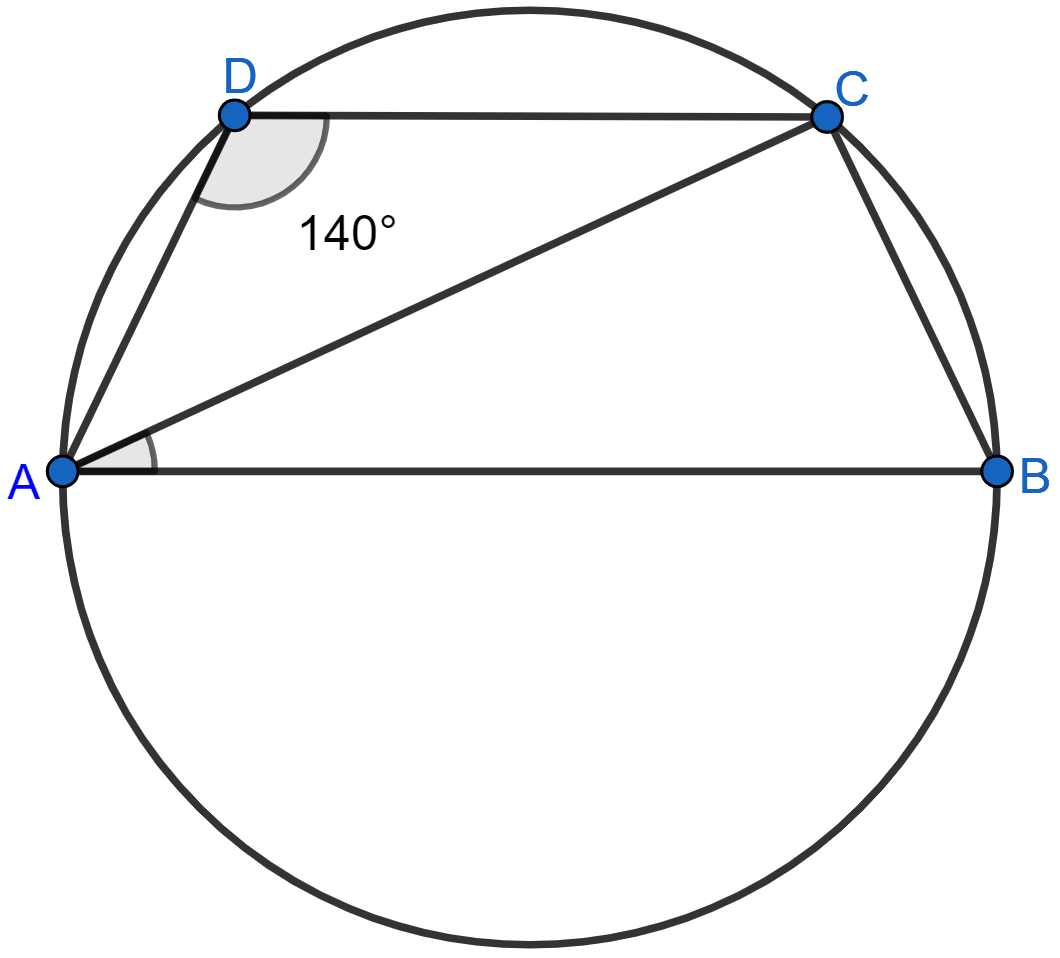
The sum of opposite angles in a quadrilateral = 180°.
∴ ∠ADC + ∠ABC = 180°
140° + ∠ABC = 180°
∠ABC = 180° - 140° = 40°.
In △ABC,
∠ACB = 90° (∵ angles in semicircle = 90°.)
Since, sum of angles in a triangle = 180°.
In △ABC,
⇒ ∠ABC + ∠ACB + ∠BAC = 180°
⇒ 40° + 90° + ∠BAC = 180°
⇒ 130° + ∠BAC = 180°
⇒ ∠BAC = 180° - 130°
⇒ ∠BAC = 50°.
Hence, Option 2 is the correct option.
Related Questions
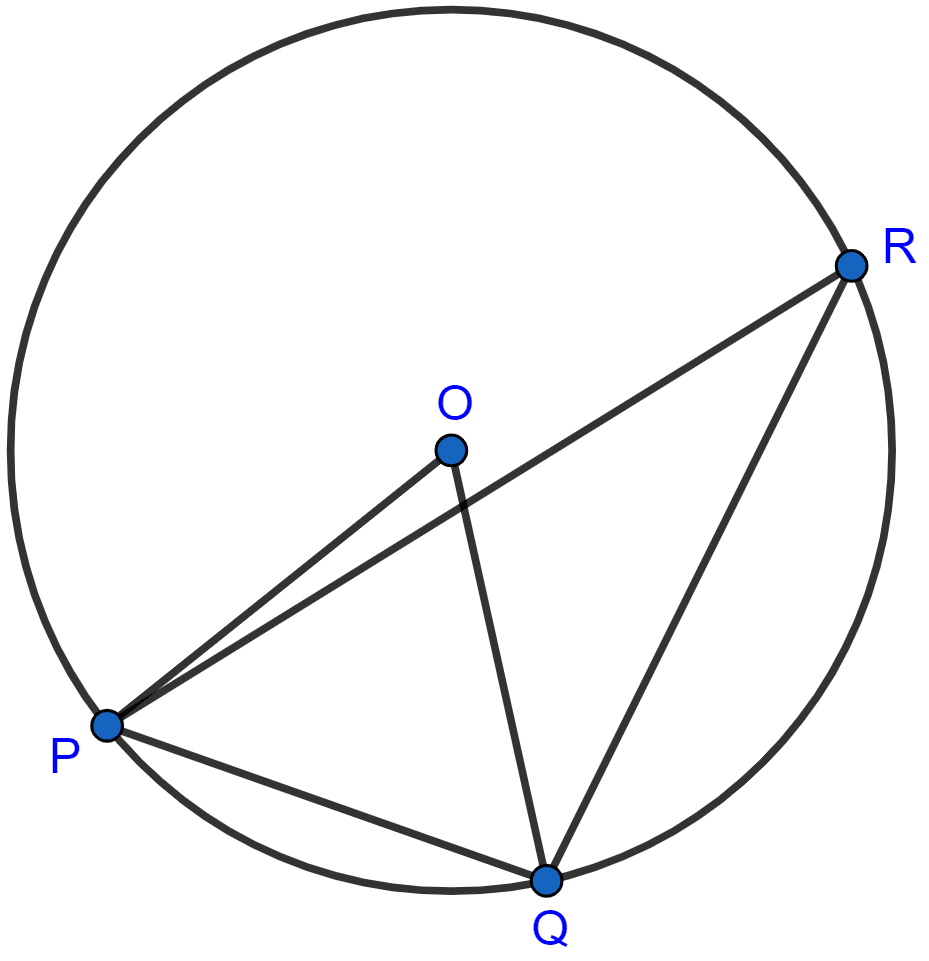
In the adjoining figure, O is the centre of the circle. If the length of the chord PQ is equal to the radius of the circle, then ∠PRQ is
60°
45°
30°
15°
In the adjoining figure, if O is the centre of the circle then the value of x is
18°
20°
24°
36°

In the adjoining figure, O is the centre of the circle. If ∠BAO = 60°, then ∠ADC is equal to
30°
45°
60°
120°

In the adjoining figure, O is the centre of the circle. If ∠OAB = 40°, then ∠ACB is equal to
50°
40°
60°
70°
