Mathematics
ABC is an isosceles triangle with AB = AC. D, E and F are mid-points of the sides BC, AB and AC respectively. Prove that line segment AD is perpendicular to EF and is bisected by it.
Answer
From figure,
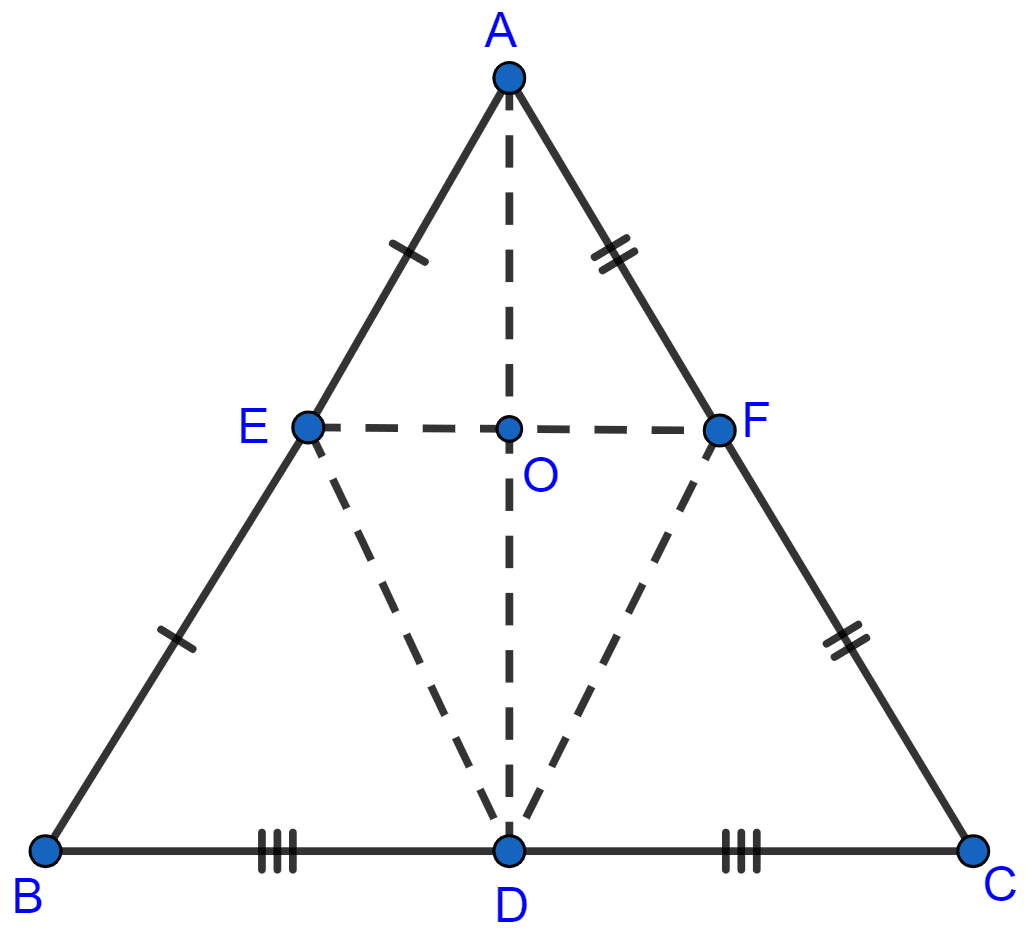
In △ABD and △ACD,
△ABC is an isosceles triangle
∴ ∠ABD = ∠ACD
Here D is the mid-point of BC
BD = CD
It is given that AB = AC
∴ △ABD ≅ △ACD (By SAS axiom of congruency)
⇒ ∠ADB = ∠ADC (By c.p.c.t.c)
From figure,
⇒ ∠ADB + ∠ADC = 180°
⇒ ∠ADB + ∠ADB = 180°
⇒ 2∠ADB = 180°
⇒ ∠ADB = 90°.
So, AD is perpendicular to BC.
D and E are mid-points of BC and AB,
By midpoint theorem,
DE || AC or,
DE || AF …….(i)
D and F are mid-points of BC and AC,
By midpoint theorem,
DF || AB or,
DF || AE …….(ii)
Using (i) and (ii) we get,
AEDF is a parallelogram.
Diagonals of parallelogram bisect each other
AD and EF bisect each other.
Since, E and F are mid-points of AB and AC,
By midpoint theorem,
EF || BC
Since, AD is perpendicular to BC and EF || BC.
∴ AD ⊥ EF.
Hence, proved that line segment AD is perpendicular to EF and is bisected by it.
Related Questions
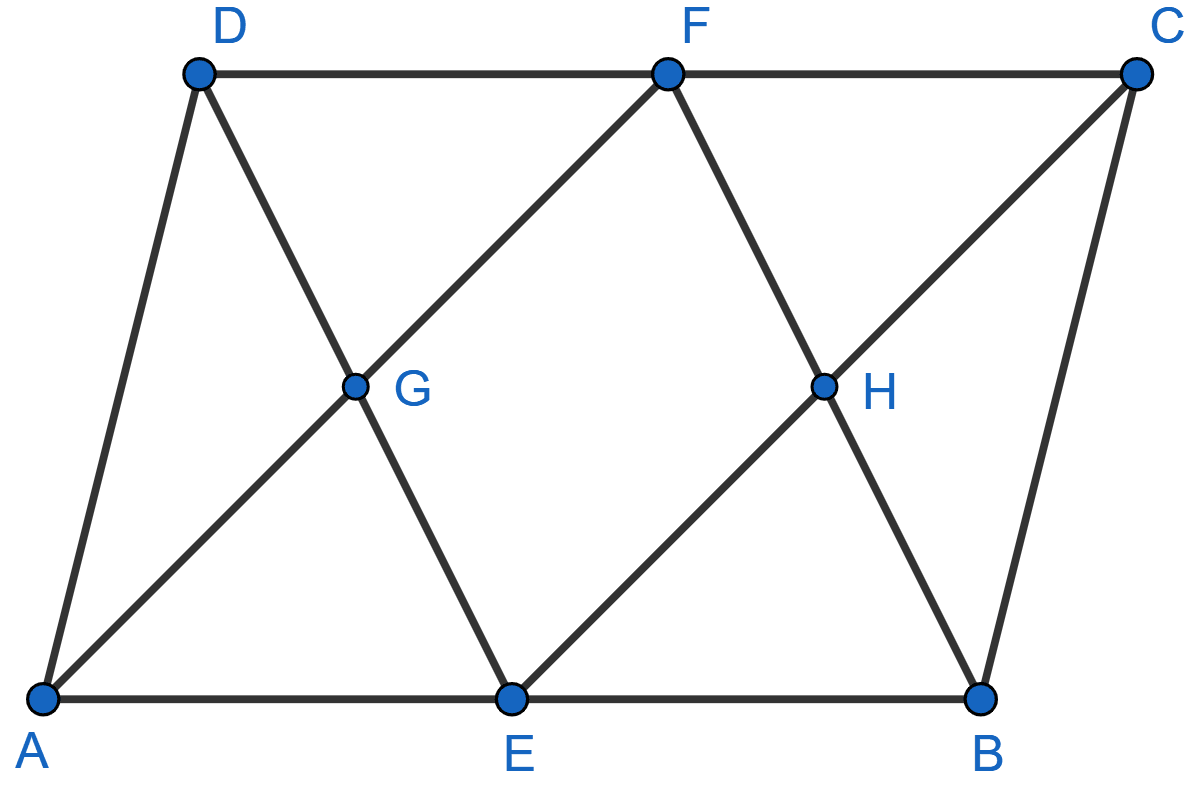
In the adjoining figure, ABCD is a parallelogram. E and F are mid-points of the sides AB and CD respectively. The straight lines AF and BF meet the straight lines ED and EC in points G and H respectively. Prove that
(i) △HEB ≅ △HCF
(ii) GEHF is a parallelogram.
In the quadrilateral given below, AB || DC || EG. If E is mid-point of AD, prove that
(i) G is midpoint of BC
(ii) 2EG = AB + CD