Mathematics
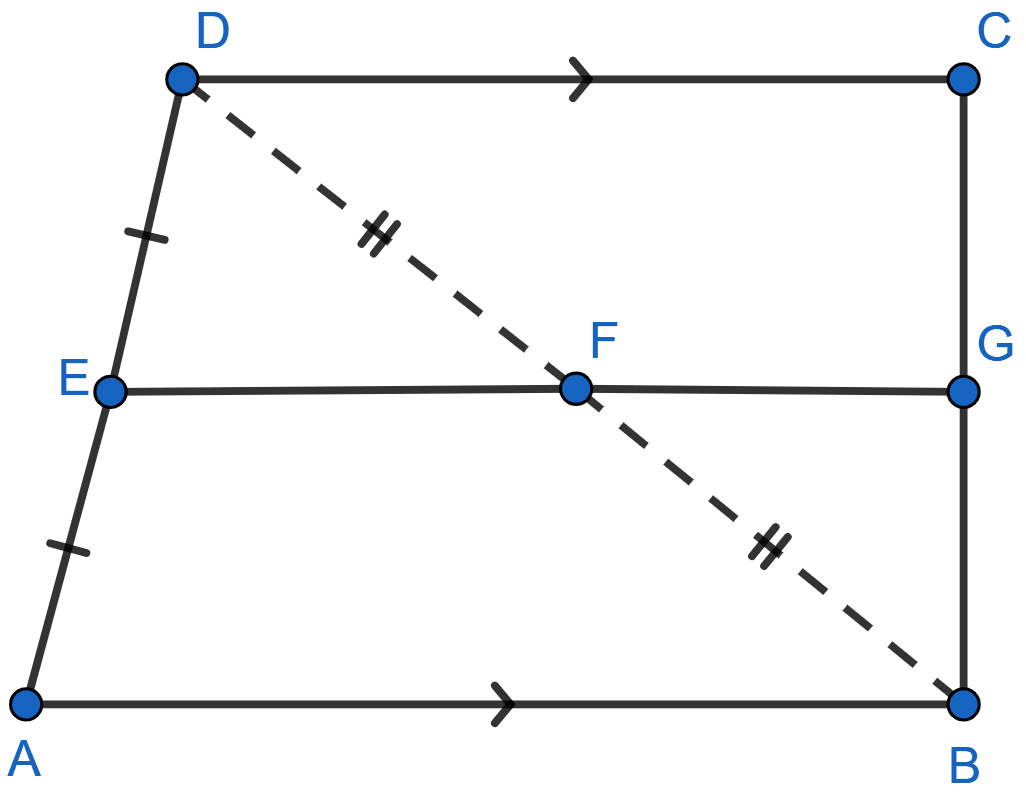
In the quadrilateral given below, AB || DC, E and F are mid-points of AD and BD respectively. Prove that
(i) G is the mid-point of BC
(ii) EG = (AB + DC).
Mid-point Theorem
63 Likes
Answer
(i) In △ABD,
E is mid-point of AD and F is mid-point of BD,
∴ EF || AB and EF = AB …….(1)
Given,
AB || CD
Since, EF || AB and AB || CD
⇒ EF || CD
⇒ EG || CD.
Since, EG || CD we can say,
In △BCD,
⇒ FG || CD
Given, F is midpoint of BD and FG || CD
∴ G is the midpoint of BC. (By converse of mid-point theorem)
Hence, proved that G is the midpoint of BC.
(ii) In △BCD,
F and G are midpoint of BD and BC respectively,
FG = CD ……….(2)
Adding eqn. (1) from part (i) and eqn (2) we get,
EF + FG = AB + CD
EG = (AB + CD).
Hence, proved that EG = (AB + CD).
Answered By
38 Likes
Related Questions
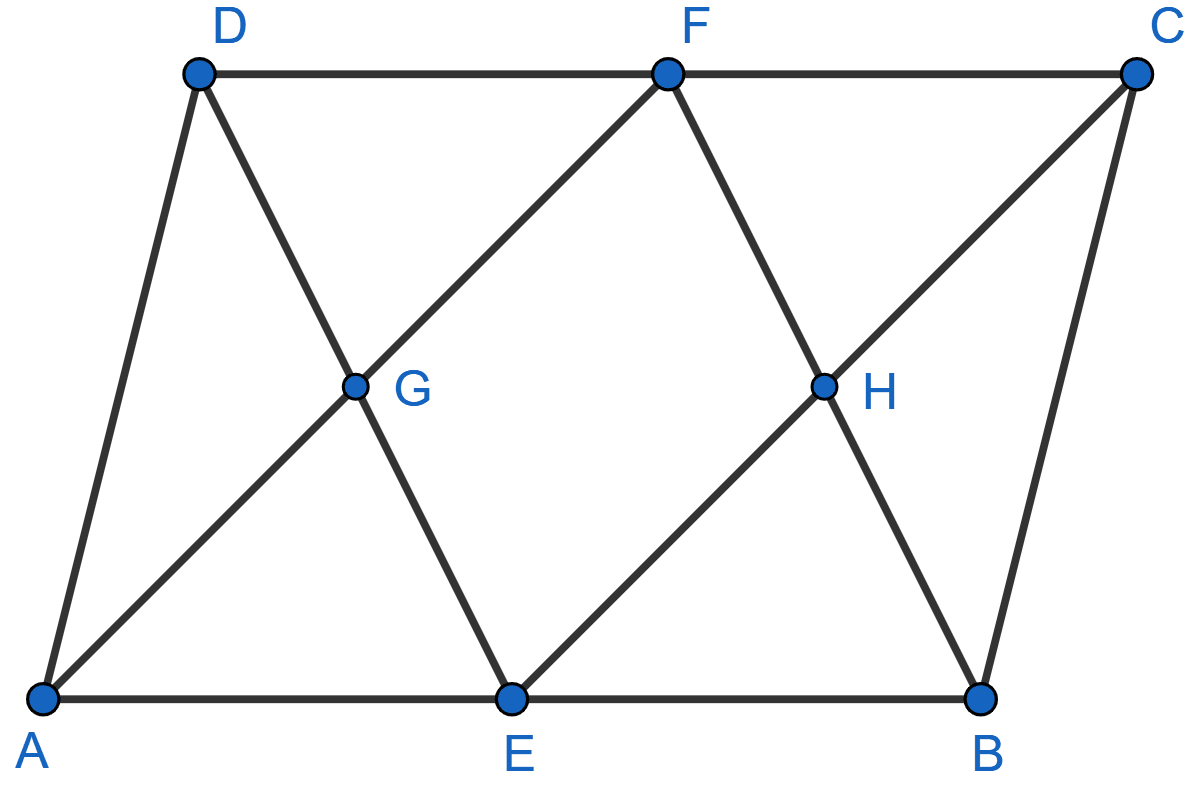
In the adjoining figure, ABCD is a parallelogram. E and F are mid-points of the sides AB and CD respectively. The straight lines AF and BF meet the straight lines ED and EC in points G and H respectively. Prove that
(i) △HEB ≅ △HCF
(ii) GEHF is a parallelogram.
ABC is an isosceles triangle with AB = AC. D, E and F are mid-points of the sides BC, AB and AC respectively. Prove that line segment AD is perpendicular to EF and is bisected by it.
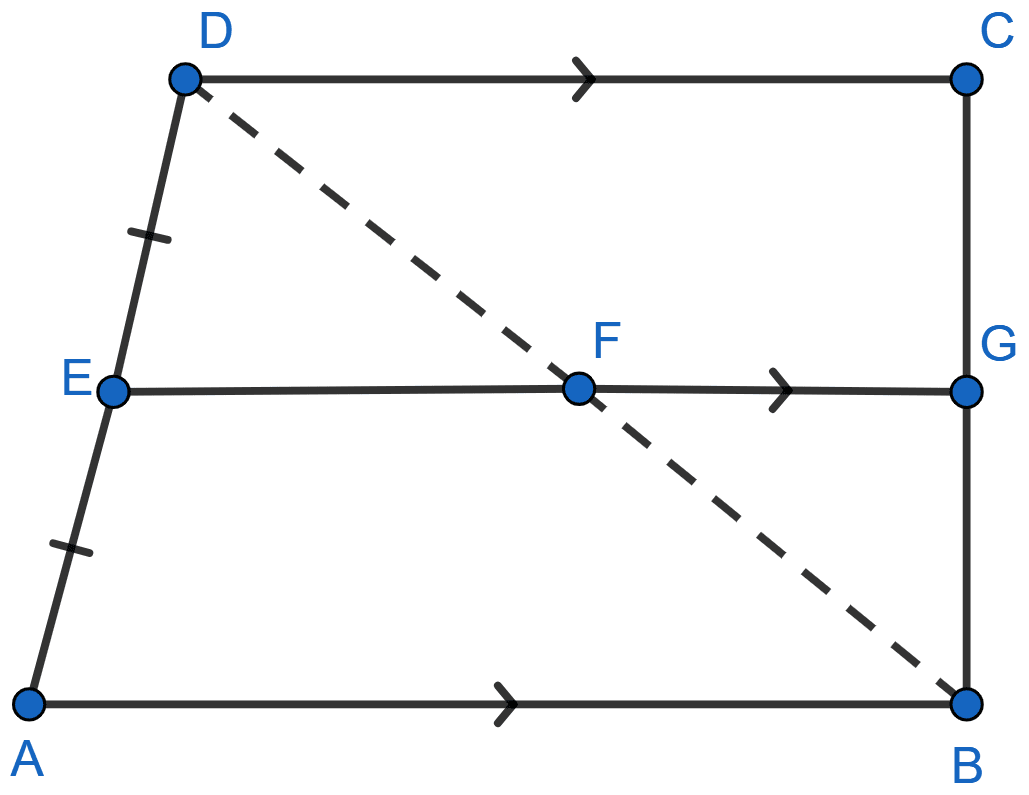
In the quadrilateral given below, AB || DC || EG. If E is mid-point of AD, prove that
(i) G is midpoint of BC
(ii) 2EG = AB + CD
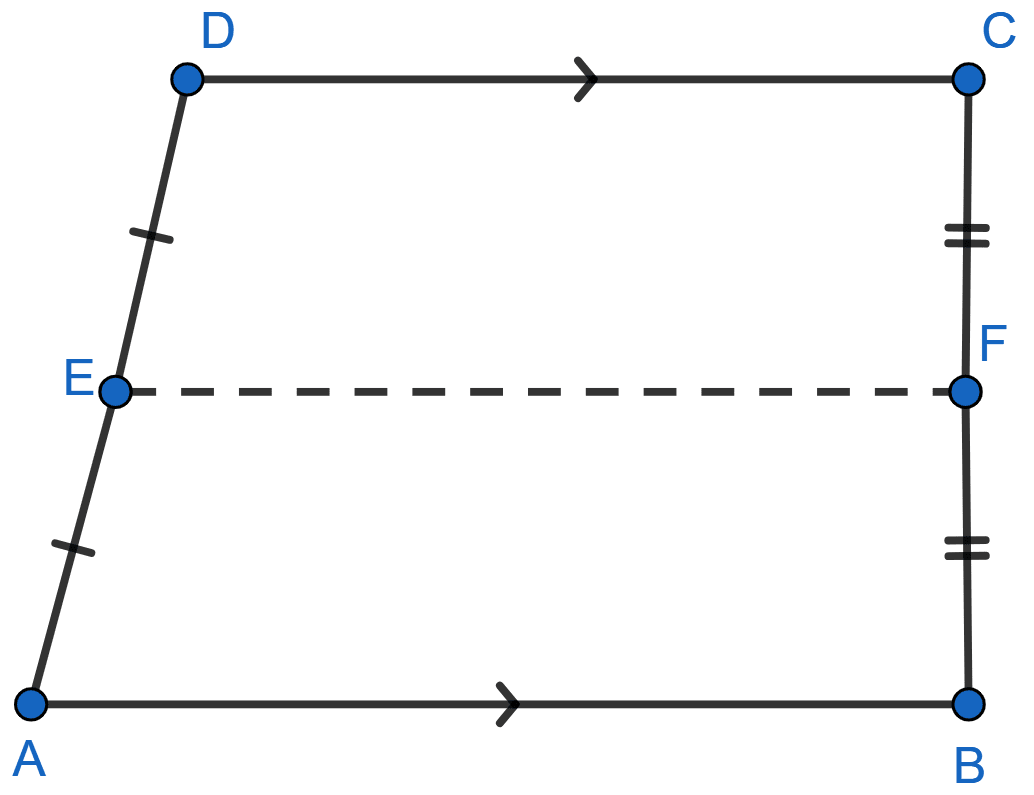
In the quadrilateral given below, AB || DC. E and F are mid-points of non-parallel sides AD and BC respectively. Calculate :
(i) EF if AB = 6 cm and DC = 4 cm
(ii) AB if DC = 8 cm and EF = 9 cm.