Mathematics
AB and CD are two parallel chords of a circle of lengths 10 cm and 4 cm respectively. If the chords lie on the same side of the centre and the distance between them is 3 cm, find the diameter of the circle.
Circles
41 Likes
Answer
Let OE = x cm.
From figure,
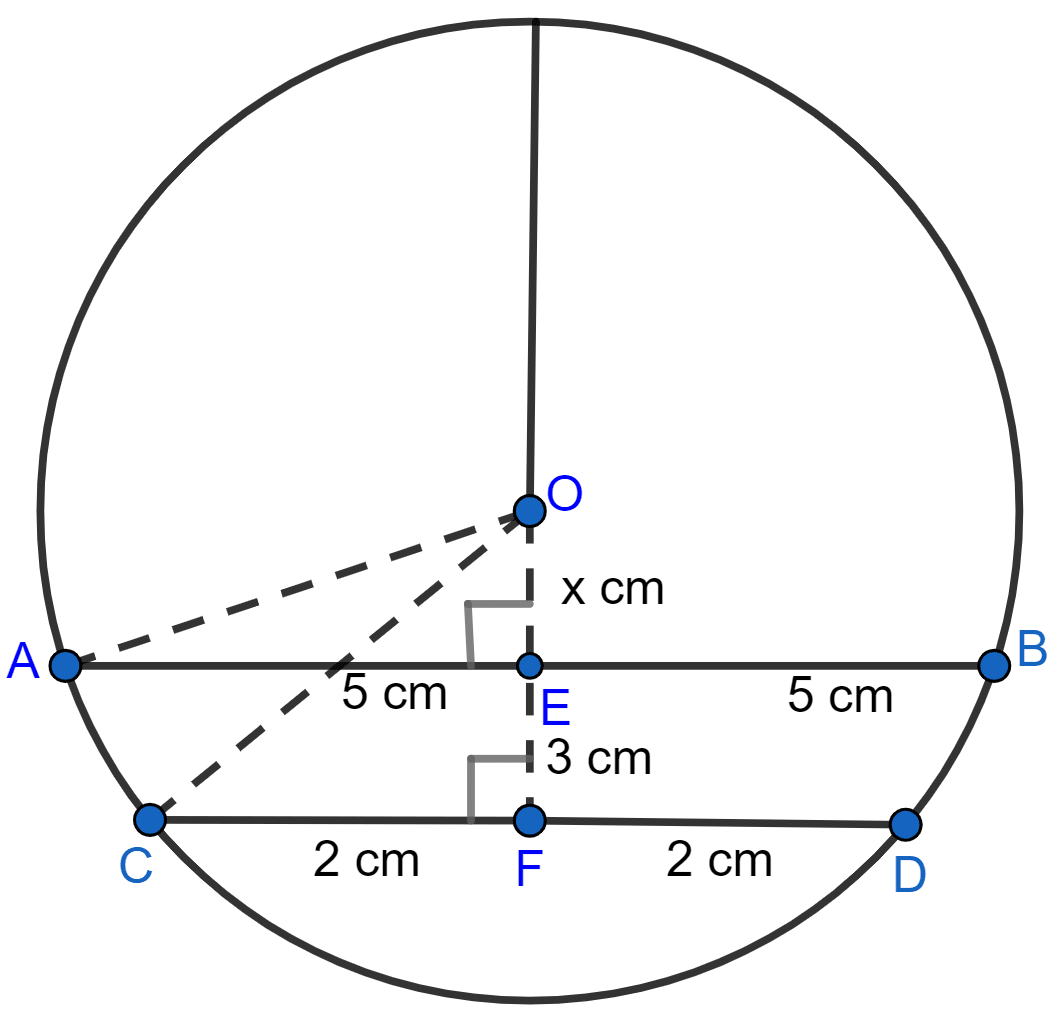
In right angle triangle OCF,
⇒ OC2 = OF2 + CF2 (By pythagoras theorem)
⇒ OC2 = (x + 3)2 + 22
⇒ OC2 = x2 + 9 + 6x + 4
⇒ OC2 = x2 + 6x + 13
Since, radius = OA = OC.
∴ OA2 = OC2 = x2 + 6x + 13.
In right angle triangle OAE,
⇒ OA2 = OE2 + AE2
⇒ x2 + 6x + 13 = x2 + 52
⇒ x2 - x2 + 6x = 25 - 13
⇒ 6x = 12
⇒ x = = 2 cm.
⇒ OC2 = x2 + 6x + 13
⇒ OC2 = 22 + 6(2) + 13
⇒ OC2 = 4 + 12 + 13
⇒ OC2 = 29
⇒ OC = cm.
Diameter = 2 × radius = 2 × cm.
Hence, diameter = cm.
Answered By
30 Likes
Related Questions
ABC is an isosceles triangle inscribed in a circle. If AB = AC = cm and BC = 24 cm, find the radius of the circle.
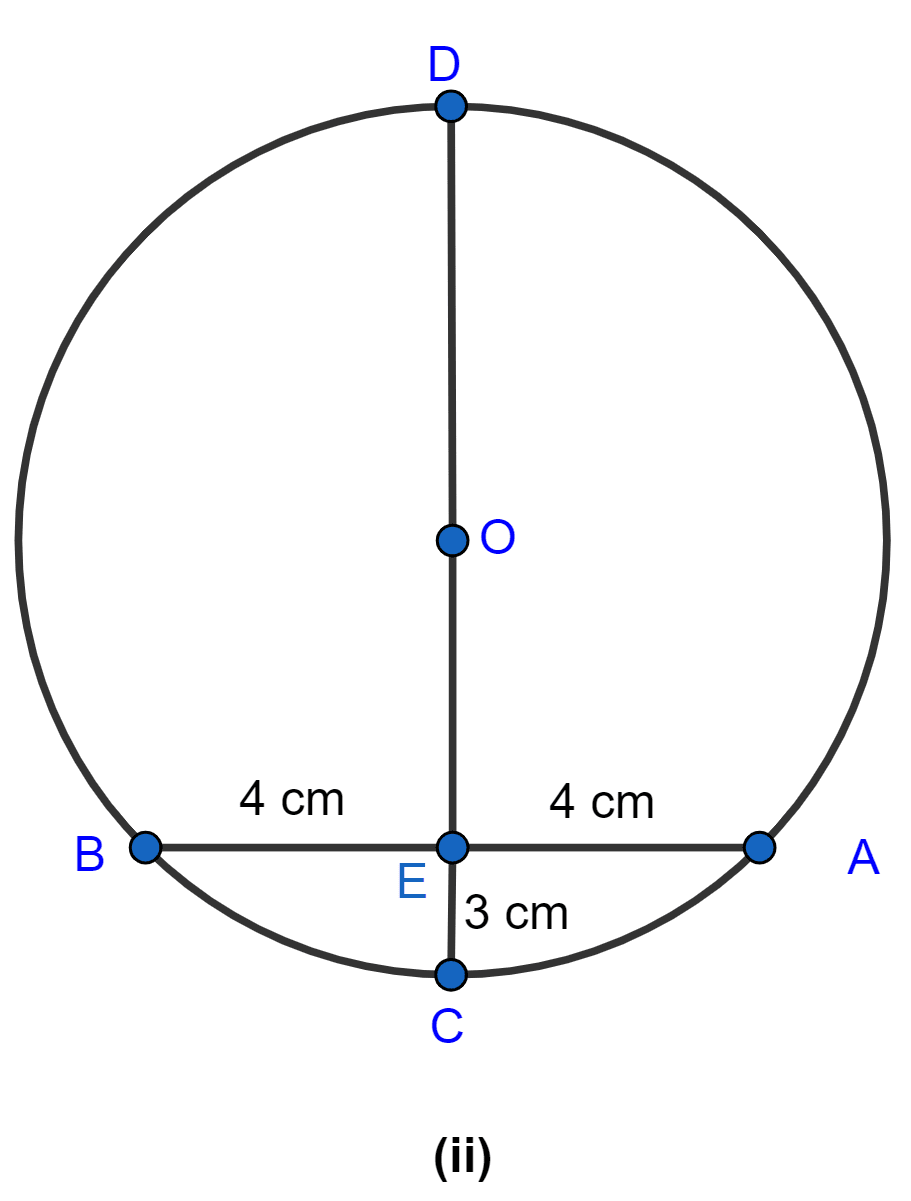
In the figure (ii) given below, CD is the diameter which meets the chord AB in E such that AE = BE = 4 cm. If CE = 3 cm, find the radius of the circle.
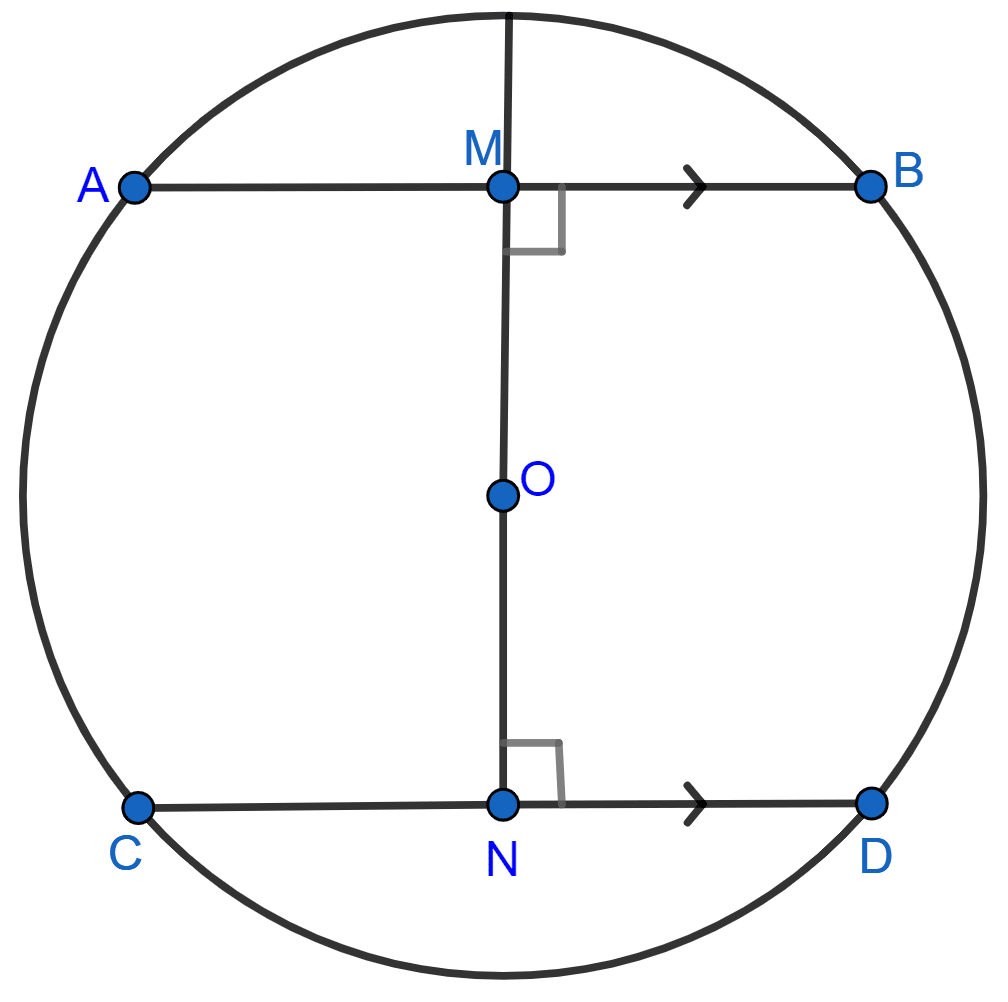
In the adjoining figure, AB and CD are two parallel chords and O is the centre. If the radius of the circle is 15 cm, find the distance MN between the two chords of length 24 cm and 18 cm respectively.
An equilateral triangle of side 6 cm is inscribed in a circle. Find the radius of the circle.