Mathematics
An equilateral triangle of side 6 cm is inscribed in a circle. Find the radius of the circle.
Circles
92 Likes
Answer
From figure,
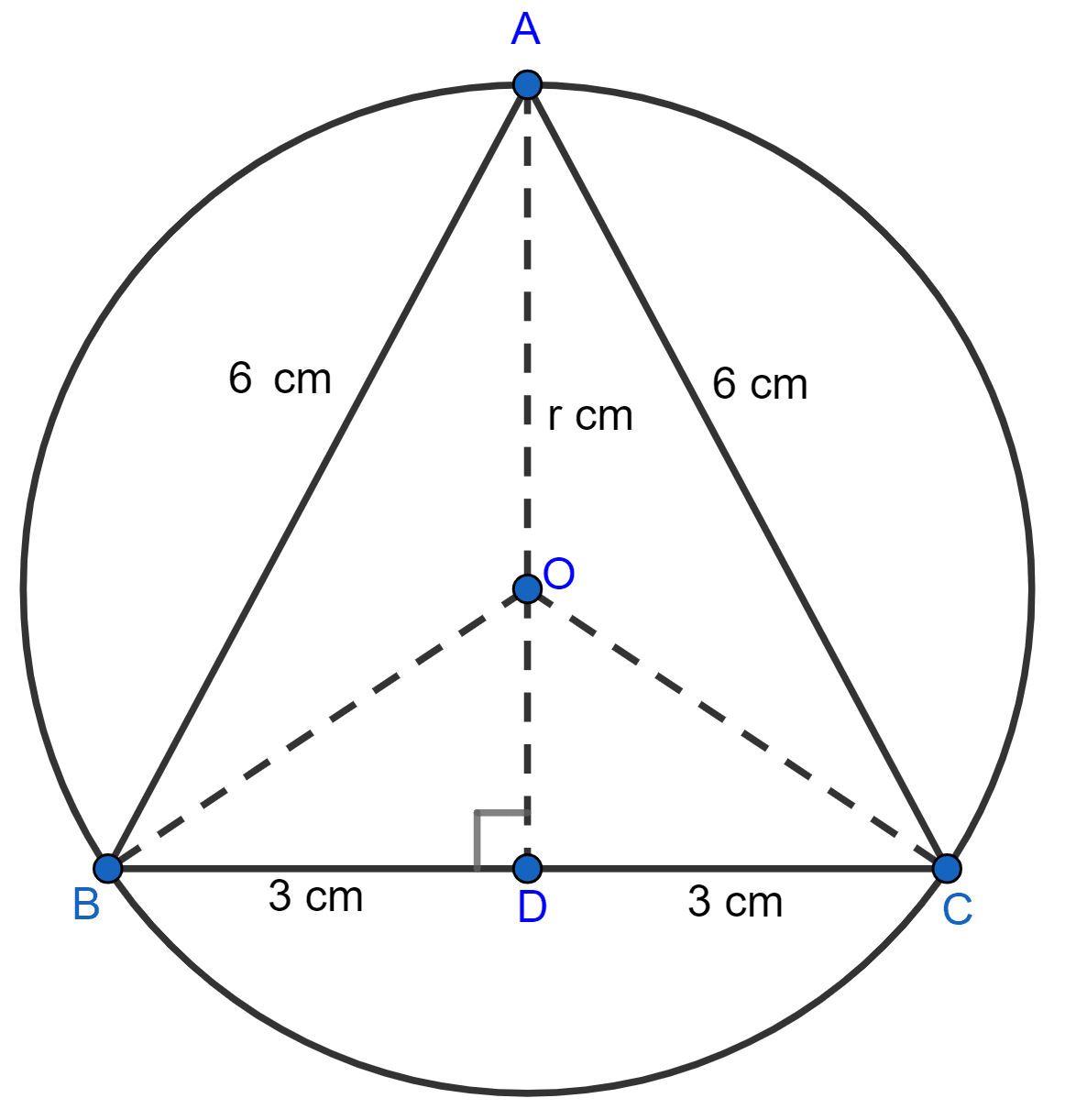
OA = radius = r cm.
BD = DC = = 3 cm (As perpendicular to a chord from the center of the circle bisects it)
In right angle triangle ABD,
⇒ AB2 = AD2 + BD2
⇒ 62 = AD2 + 32
⇒ AD2 = 36 - 9
⇒ AD2 = 27
⇒ AD = = cm.
OD = AD - AO = cm.
In right angle triangle OBD,
⇒ OB = radius = r cm.
⇒ OB2 = OD2 + BD2
⇒ r2 = 2 + 32
⇒ r2 = 27 + r2 - r + 9
⇒ r2 - r2 + r = 36
⇒ r = 36
⇒ r = cm.
Hence, radius = cm.
Answered By
35 Likes
Related Questions
AB and CD are two parallel chords of a circle of lengths 10 cm and 4 cm respectively. If the chords lie on the same side of the centre and the distance between them is 3 cm, find the diameter of the circle.
ABC is an isosceles triangle inscribed in a circle. If AB = AC = cm and BC = 24 cm, find the radius of the circle.
AB is a diameter of a circle. M is a point in AB such that AM = 18 cm and MB = 8 cm. Find the length of the shortest chord through M.
A rectangle with one side of length 4 cm is inscribed in a circle of diameter 5 cm. Find the area of rectangle.