Mathematics
ABC is an isosceles triangle inscribed in a circle. If AB = AC = cm and BC = 24 cm, find the radius of the circle.
Circles
67 Likes
Answer
From figure,
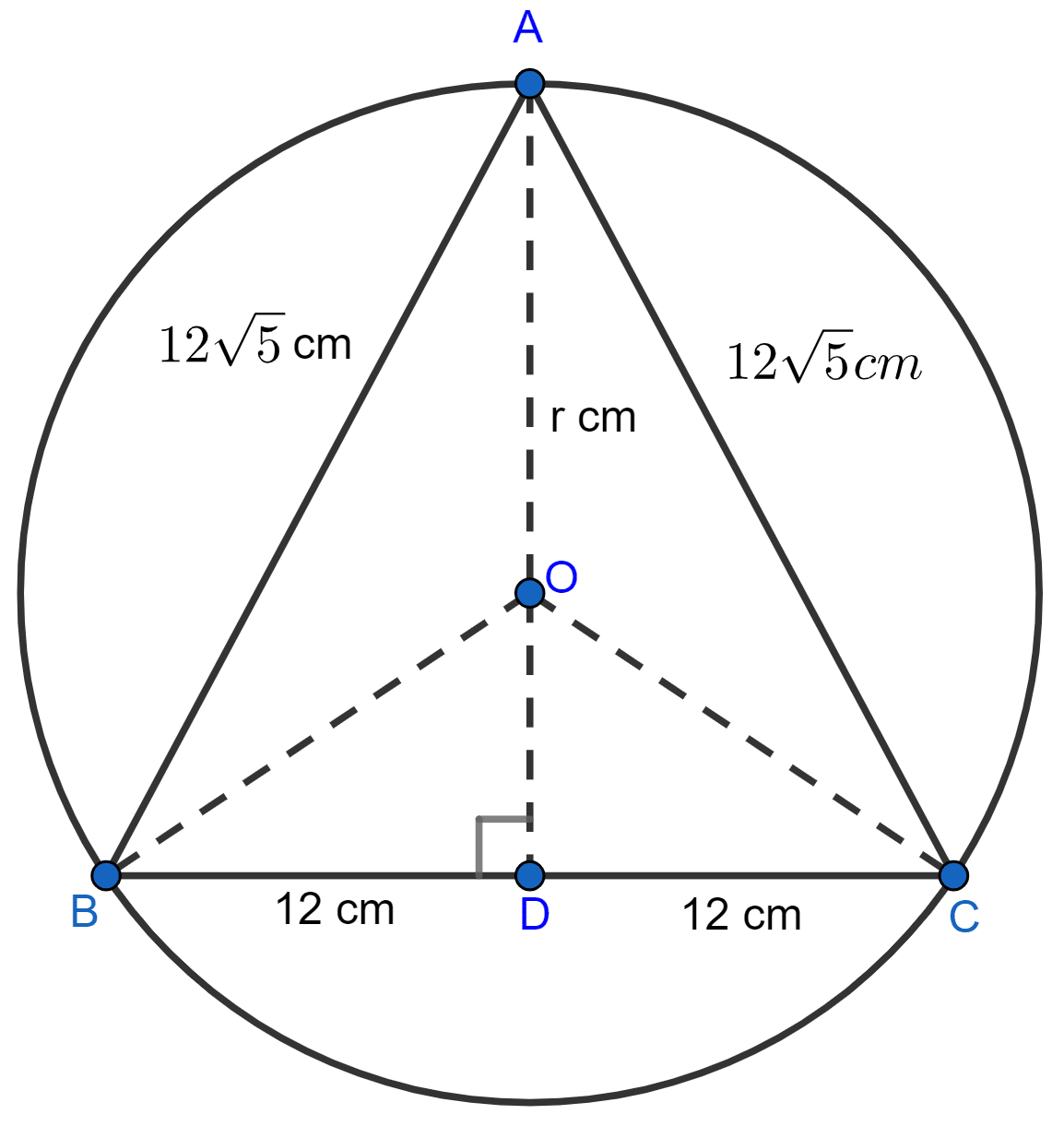
OA = radius = r cm.
BD = DC = = 12 cm (As perpendicular to a chord from the center of the circle bisects it)
In right angle triangle ABD,
OD = AD - OA = (24 - r) cm.
In right angle triangle OBD,
⇒ OB = radius = r cm.
⇒ OB2 = OD2 + BD2
⇒ r2 = (24 - r)2 + 122
⇒ r2 = 576 + r2 - 48r + 144
⇒ r2 - r2 + 48r = 720
⇒ 48r = 720
⇒ r = = 15 cm.
Hence, radius = 15 cm.
Answered By
51 Likes
Related Questions
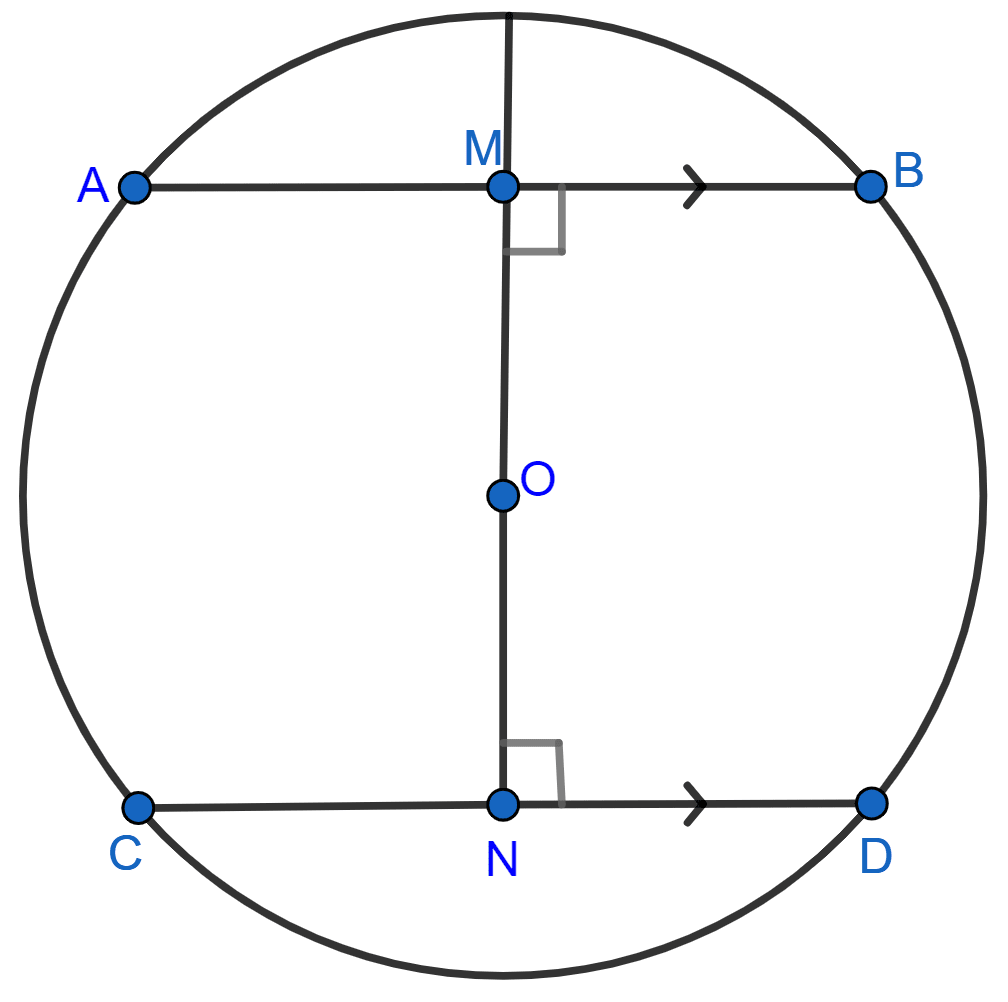
In the adjoining figure, AB and CD are two parallel chords and O is the centre. If the radius of the circle is 15 cm, find the distance MN between the two chords of length 24 cm and 18 cm respectively.
AB and CD are two parallel chords of a circle of lengths 10 cm and 4 cm respectively. If the chords lie on the same side of the centre and the distance between them is 3 cm, find the diameter of the circle.
An equilateral triangle of side 6 cm is inscribed in a circle. Find the radius of the circle.
AB is a diameter of a circle. M is a point in AB such that AM = 18 cm and MB = 8 cm. Find the length of the shortest chord through M.