Mathematics
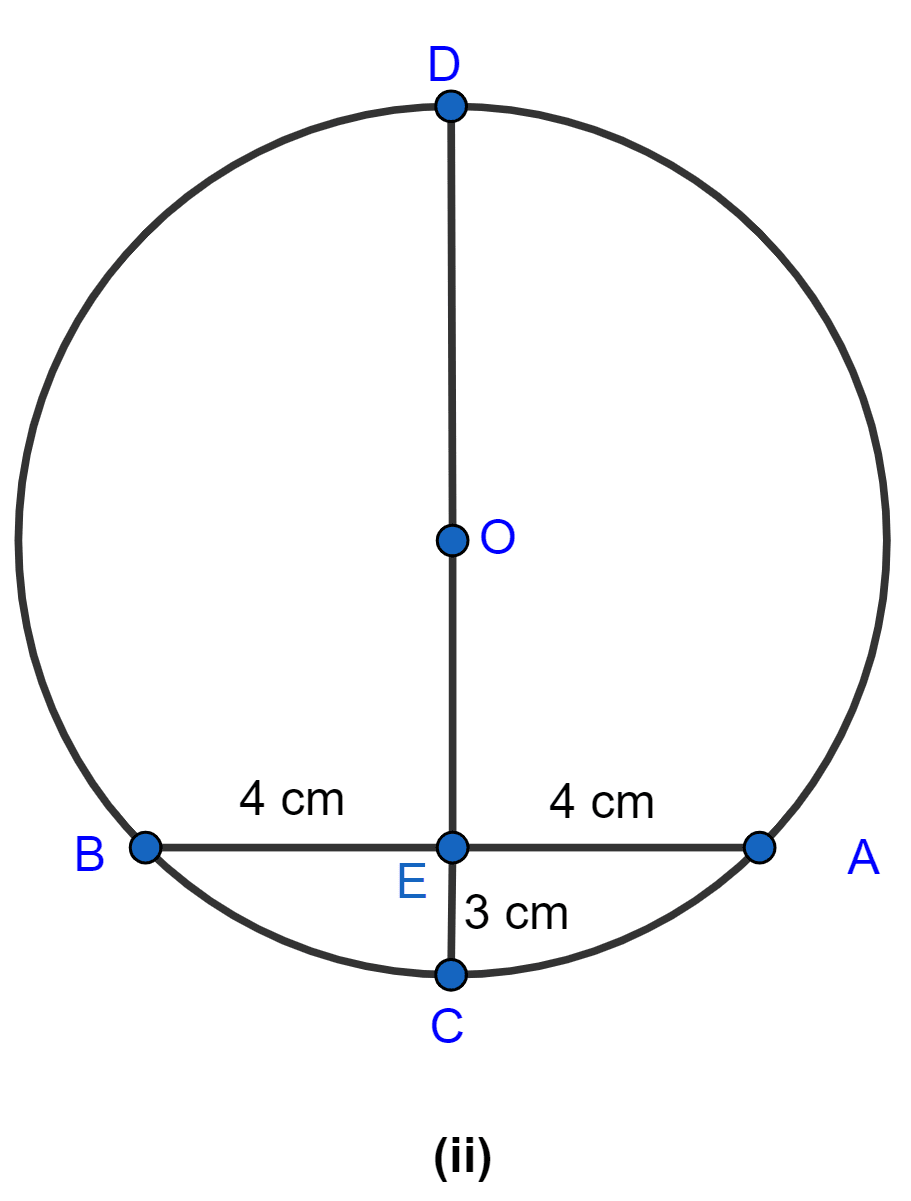
In the figure (ii) given below, CD is the diameter which meets the chord AB in E such that AE = BE = 4 cm. If CE = 3 cm, find the radius of the circle.
Circles
78 Likes
Answer
Given,
AB = 8 cm, EC = 3 cm
Let radius OB = OC = r
OE = (r - 3) cm.
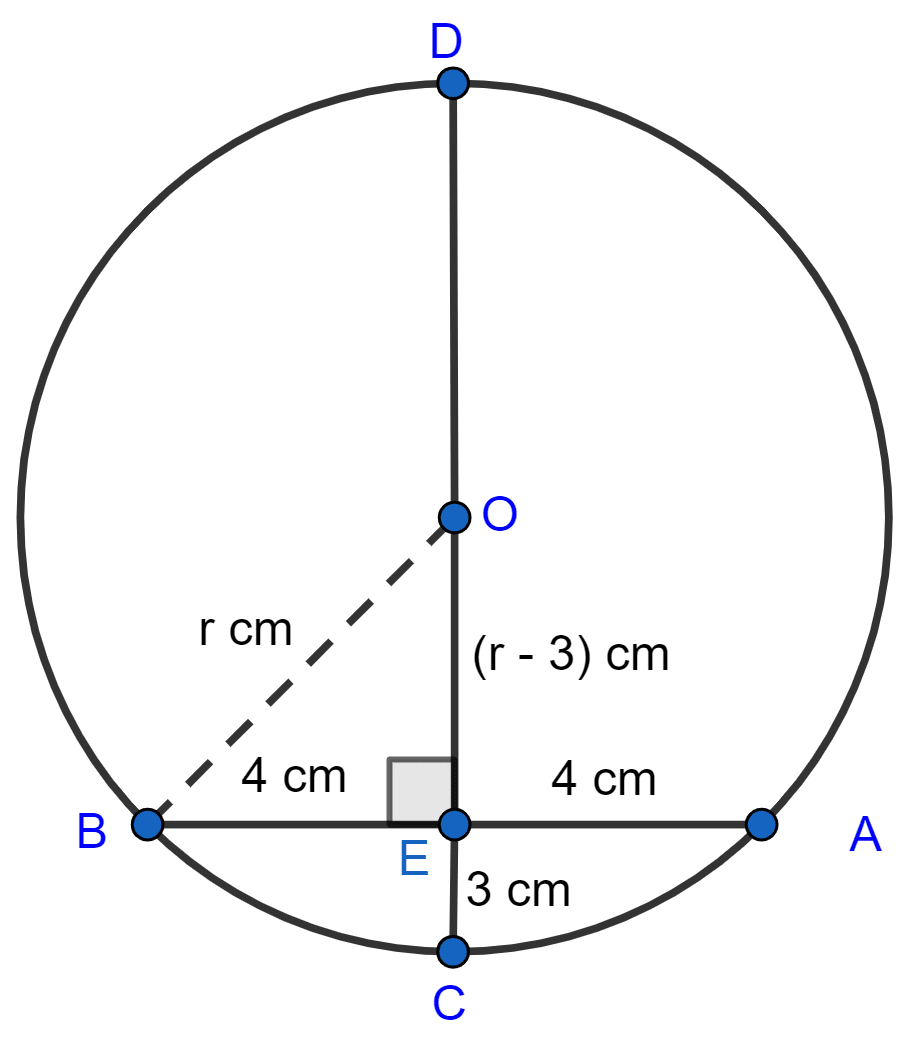
Since, chord AB is bisected by OE so OE ⊥ AB (As straight line drawn from the centre of circle to bisect a chord, is perpendicular to it.)
Now in right ∆OBE,
⇒ OB2 = BE2 + OE2
⇒ r2 = 42 + (r – 3)2
⇒ r2 = 16 + r2 – 6r + 9
⇒ r2 - r2 + 6r = 16 + 9
⇒ 6r = 25
⇒ r = cm.
Hence, radius = cm.
Answered By
62 Likes
Related Questions
In a circle of radius 5 cm, AB and CD are two parallel chords of length 8 cm and 6 cm respectively. Calculate the distance between the chords, if they are on
(i) the same side of the centre
(ii) the opposite sides of the centre.
In figure (i) given below, O is the center of the circle. AB and CD are two chords of the circle. OM is perpendicular to AB and ON is perpendicular to CD. AB = 24 cm, OM = 5 cm, ON = 12 cm. Find the :
(i) radius of the circle
(ii) length of chord CD.

In the adjoining figure, AB and CD are two parallel chords and O is the centre. If the radius of the circle is 15 cm, find the distance MN between the two chords of length 24 cm and 18 cm respectively.
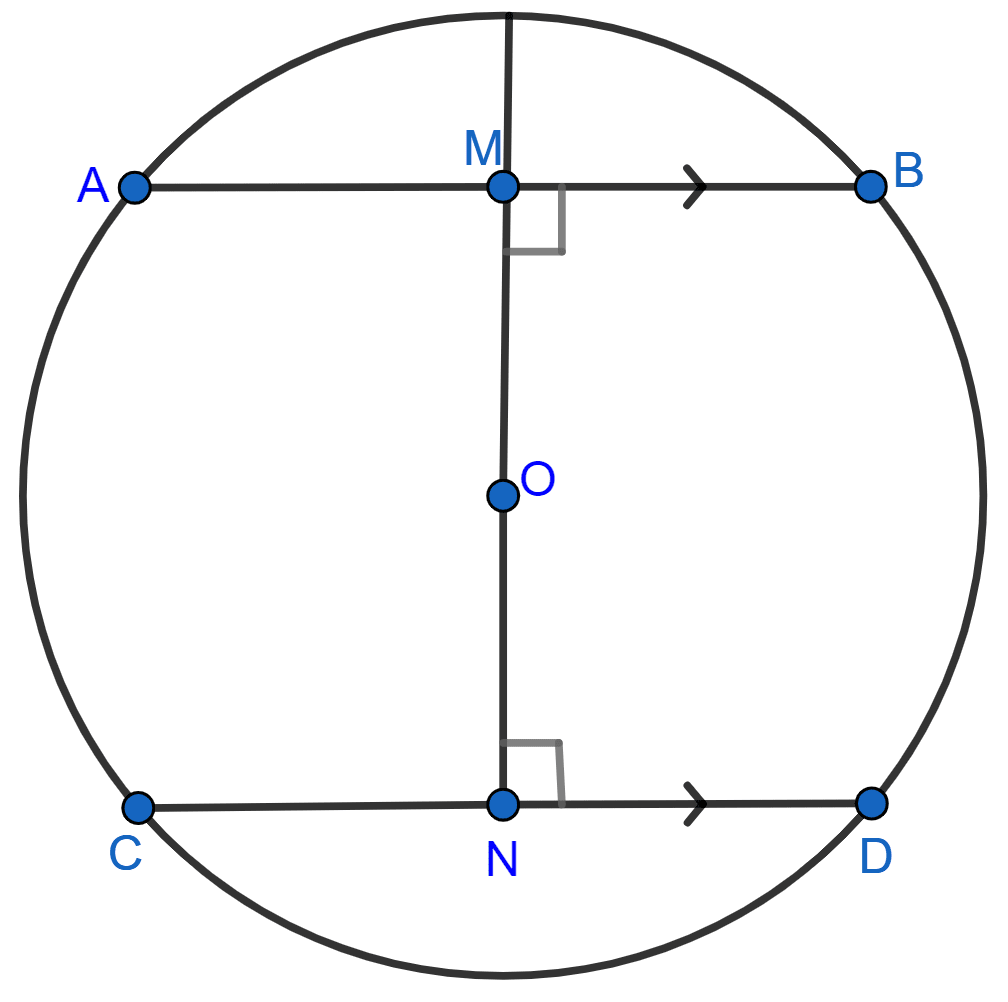
AB and CD are two parallel chords of a circle of lengths 10 cm and 4 cm respectively. If the chords lie on the same side of the centre and the distance between them is 3 cm, find the diameter of the circle.