Mathematics
A triangle ABC is inscribed in a circle. The bisectors of angle BAC, ABC and ACB meet the circumcircle of the triangle at points P, Q and R respectively. Prove that : (i) ∠ABC = 2∠APQ (ii) ∠ACB = 2∠APR (iii) ∠QPR = 90° - ∠BAC.
Related Questions
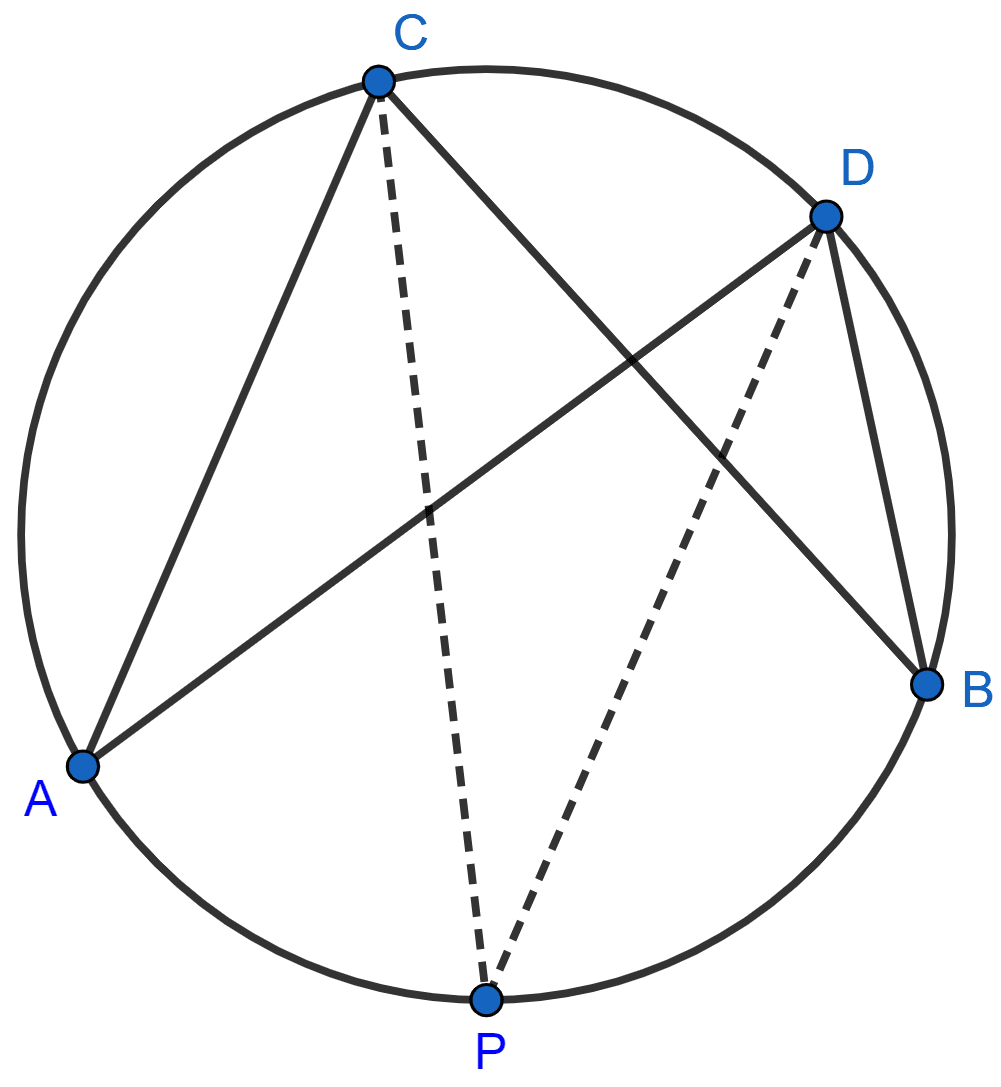
In the figure, given below, CP bisects angle ACB. Show that DP bisects angle ADB.
In the figure, given below, AD = BC, ∠BAC = 30° and ∠CBD = 70°. Find :
(i) ∠BCD
(ii) ∠BCA
(iii) ∠ABC
(iv) ∠ADB

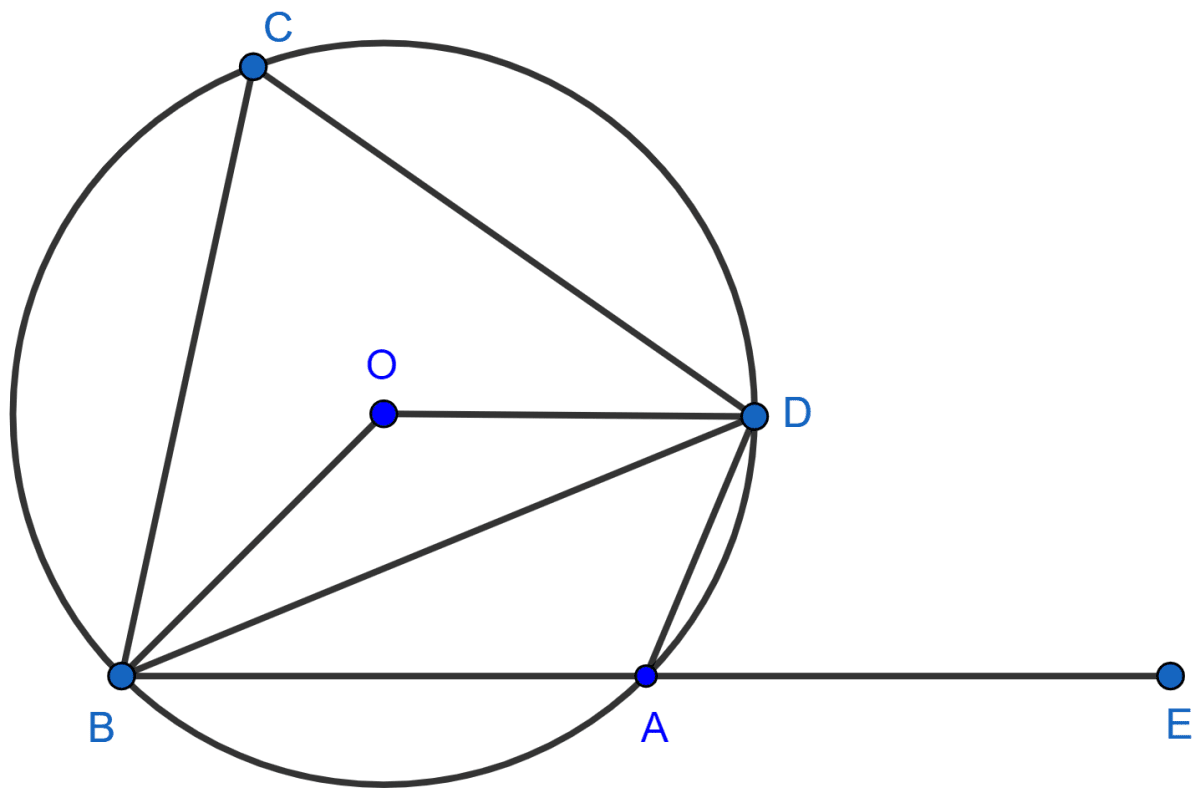
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°. Find :
(i) ∠OBD
(ii) ∠AOB
(iii) ∠BED

In the figure given, O is the centre of the circle. ∠DAE = 70°. Find giving suitable reasons, the measure of
(i) ∠BCD
(ii) ∠BOD
(iii) ∠OBD