Mathematics
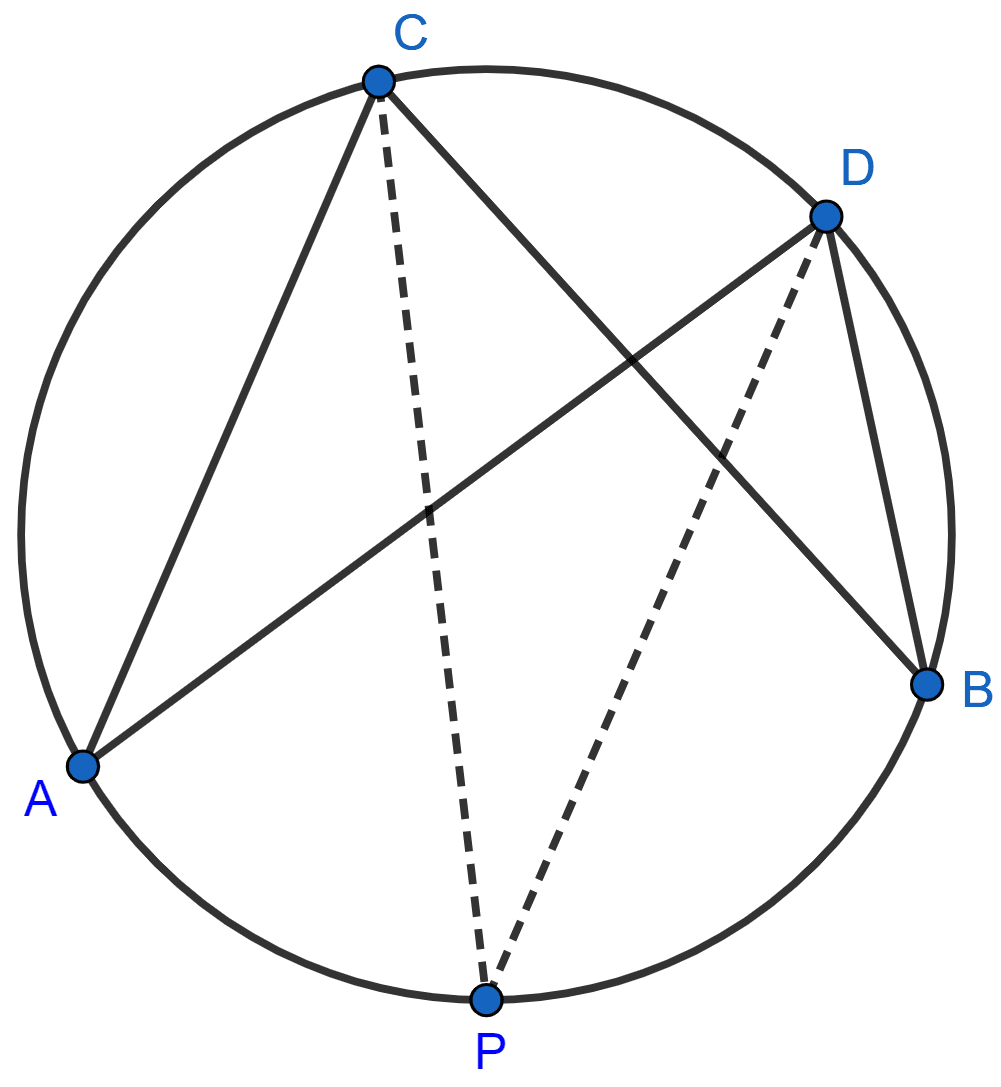
In the figure, given below, CP bisects angle ACB. Show that DP bisects angle ADB.
Circles
4 Likes
Answer
Since, CP is the bisector of ∠ACB,
∴ ∠ACP = ∠BCP ………(1)
We know that,
Angles in same segment are equal.
∴ ∠ACP = ∠ADP ……….(2)
∠BCP = ∠BDP ………..(3)
From (1) and (2) we get,
∠BCP = ∠ADP ………..(4)
From (3) and (4) we get,
∠ADP = ∠BDP.
∴ DP is the bisector of ∠ADB.
Hence, proved that DP is the bisector of ∠ADB.
Answered By
2 Likes
Related Questions
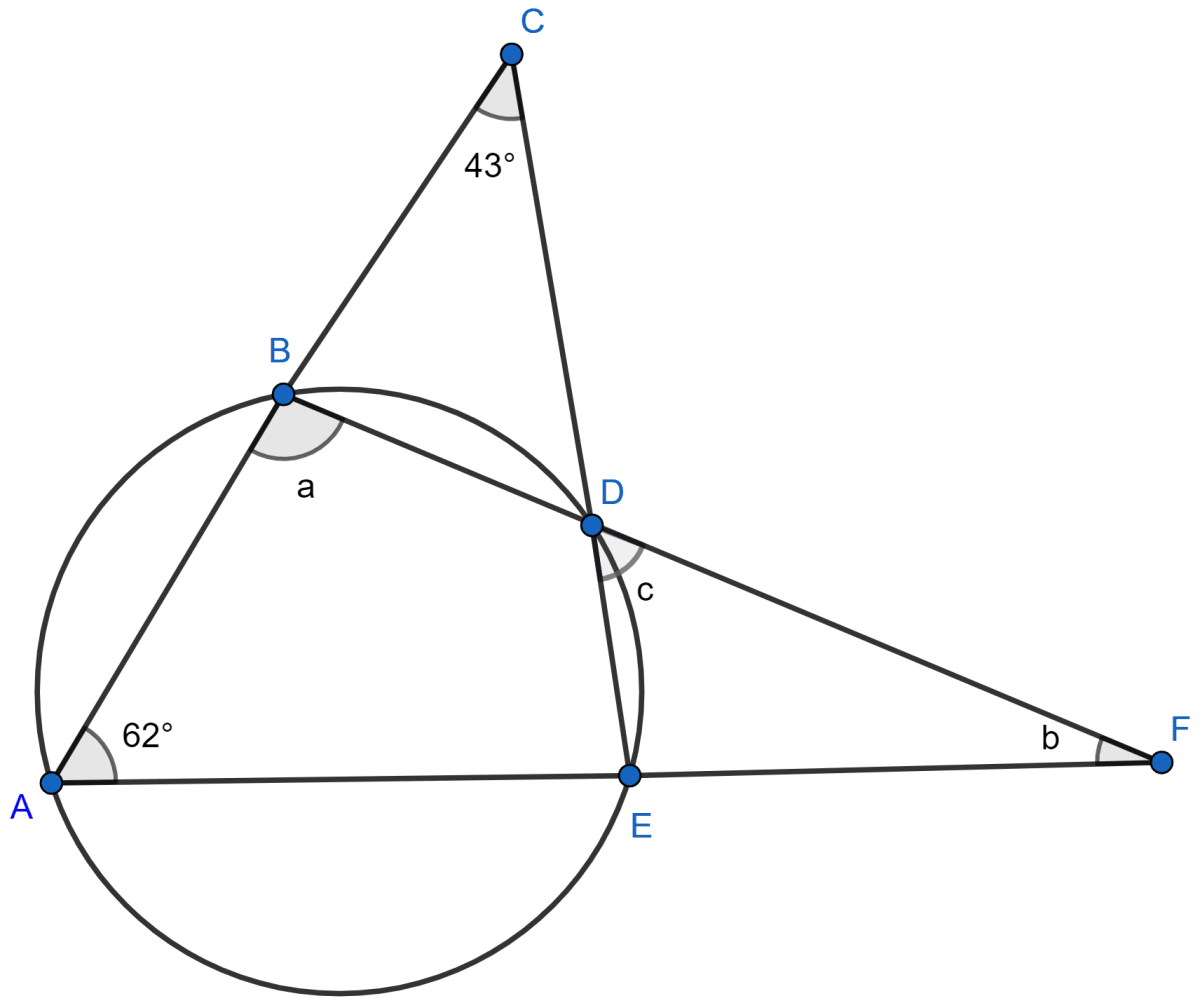
In the given figure, ∠ACE = 43° and ∠CAF = 62°; find the values of a, b and c.
In the given figure, AB is parallel to DC, ∠BCE = 80° and ∠BAC = 25°.
Find :
(i) ∠CAD
(ii) ∠CBD
(iii) ∠ADC

In the figure, given below, AD = BC, ∠BAC = 30° and ∠CBD = 70°. Find :
(i) ∠BCD
(ii) ∠BCA
(iii) ∠ABC
(iv) ∠ADB

In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°. Find :
(i) ∠OBD
(ii) ∠AOB
(iii) ∠BED
