Mathematics
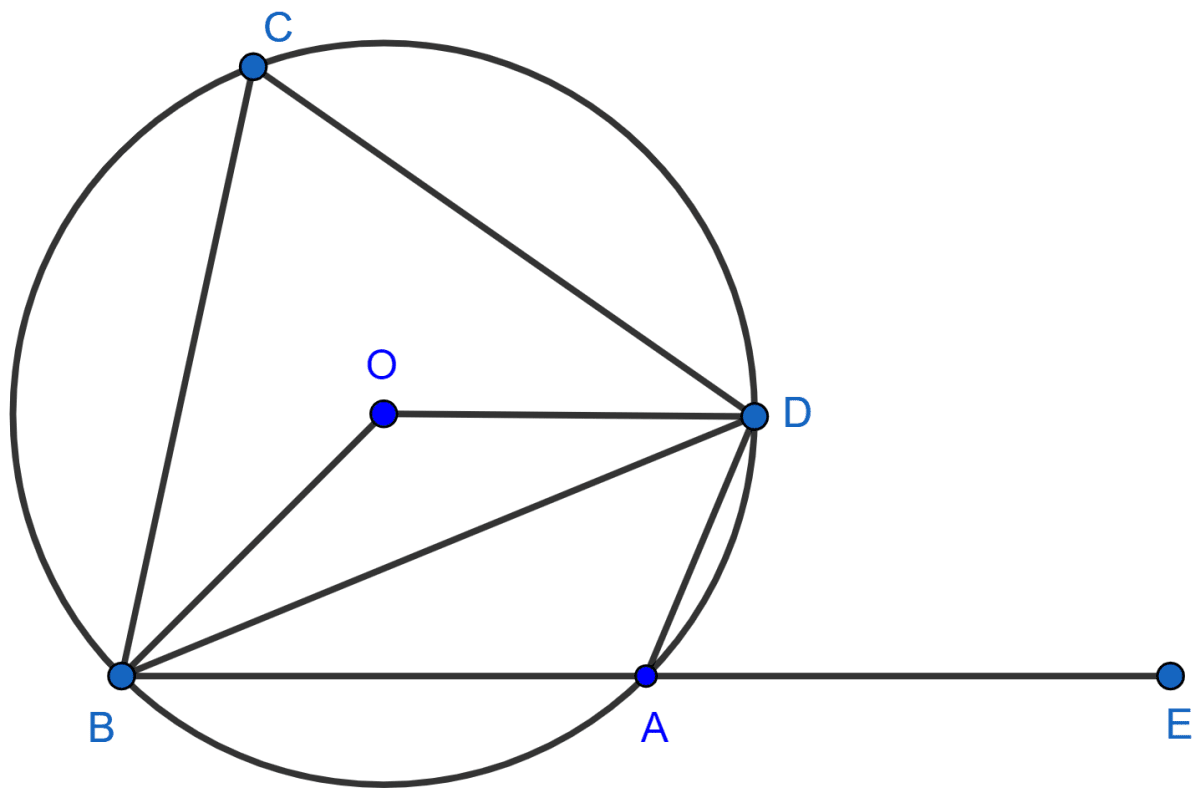
In the figure, given below, AD = BC, ∠BAC = 30° and ∠CBD = 70°. Find :
(i) ∠BCD
(ii) ∠BCA
(iii) ∠ABC
(iv) ∠ADB

Circles
7 Likes
Answer
We know that,
Angles in same segment are equal.
∴ ∠CAD = ∠CBD = 70°.
From figure,
∠BAD = ∠BAC + ∠CAD = 30° + 70° = 100°.
(i) As sum of opposite angles in cyclic quadrilateral = 180°.
In cyclic quadrilateral ABCD,
⇒ ∠BCD + ∠BAD = 180°
⇒ ∠BCD + 100° = 180°
⇒ ∠BCD = 180° - 100° = 80°.
Hence, ∠BCD = 80°.
(ii) Since, AD = BC.
∴ ABCD is an isosceles trapezium and AB || DC.
∠DCA = ∠BAC = 30° [Alternate angles]
From figure,
∠BCA = ∠BCD - ∠DCA = 80° - 30° = 50°.
Hence, ∠BCA = 50°.
(iii) As angles in same segment are equal.
∠ABD = ∠DCA = 30°
From figure,
∠ABC = ∠ABD + ∠CBD = 30° + 70° = 100°.
Hence, ∠ABC = 100°.
(iv) As angles in same segment are equal.
∠ADB = ∠BCA = 50°.
Hence, ∠ADB = 50°.
Answered By
5 Likes
Related Questions
In the given figure, AB is parallel to DC, ∠BCE = 80° and ∠BAC = 25°.
Find :
(i) ∠CAD
(ii) ∠CBD
(iii) ∠ADC

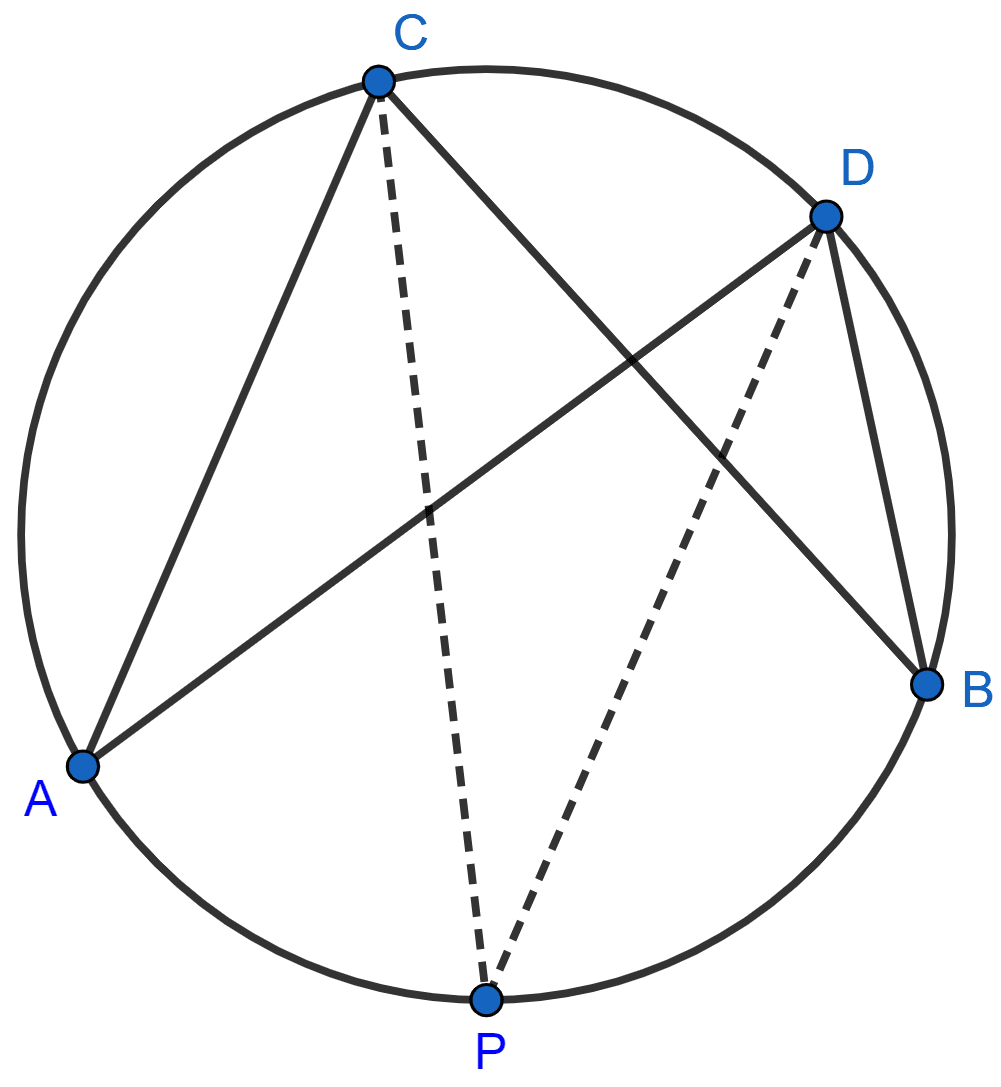
In the figure, given below, CP bisects angle ACB. Show that DP bisects angle ADB.
In the given figure, AD is a diameter. O is the centre of the circle. AD is parallel to BC and ∠CBD = 32°. Find :
(i) ∠OBD
(ii) ∠AOB
(iii) ∠BED

In the figure given, O is the centre of the circle. ∠DAE = 70°. Find giving suitable reasons, the measure of
(i) ∠BCD
(ii) ∠BOD
(iii) ∠OBD