A rocket is in the form of a right circular cylinder closed at the lower end and surmounted by a cone with the same radius as that of the cylinder. The diameter and the height of the cylinder are 6 cm and 12 cm respectively. If the slant height of the conical portion is 5 cm, find the total surface area and the volume of the rocket. (Use π = 3.14).

The below figure shows the rocket:

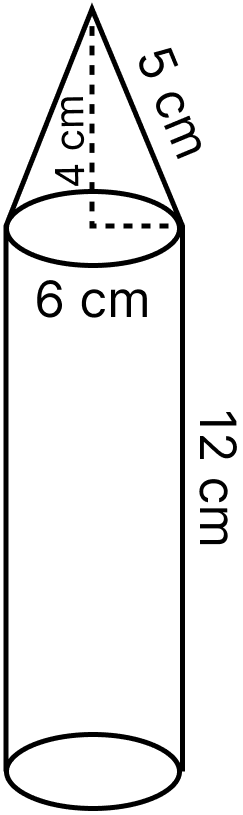
Given,

Height of cylindrical portion (H) = 12 cm.

Radius of cylinder and cone = $\dfrac{\text{Diameter}}{2} = \dfrac{6}{2}$ = 3 cm.

Slant height of cone (l) = 5 cm.

⇒ h² = l² - r²
⇒ h² = 5² - 3²
⇒ h² = 25 - 9
⇒ h² = 16
⇒ h = $\sqrt{16}$ = 4 cm.

Total surface area of rocket (S) = Curved surface area of cylinder + Base area of cylinder + Curved surface area of cone.

$\therefore S = 2πrH + πr^2 + πrl \\[1em] = πr(2H + r + l) \\[1em] = 3.14 \times 3 \times (2 \times 12 + 3 + 5) \\[1em] = 9.42 \times 32 \\[1em] = 301.44 \text{ cm}^2.$

Volume of the rocket (V) = Volume of cone + Volume of cylinder.

$\therefore V = \dfrac{1}{3}πr^2h + πr^2H \\[1em] = πr^2\Big(\dfrac{h}{3} + H) \\[1em] = 3.14 \times 3^2 \times \Big(\dfrac{4}{3} + 12\Big) \\[1em] = 3.14 \times 3^2 \times \Big(\dfrac{4 + 36}{3} \Big) \\[1em] = 3.14 \times 9 \times \dfrac{40}{3} \\[1em] = 376.8 \text{ cm}^3.$

Hence, the total surface area of rocket is 301.44 cm² and volume is 376.8 cm³.