Mathematics
A buoy is made in the form of a hemisphere surmounted by a right cone whose circular base coincides with the plane surface of the hemisphere. The radius of the base of the cone is 3.5 metres and its volume is of the hemisphere. Calculate the height of the cone and the surface area of the buoy correct to 2 places of decimal.
Mensuration
44 Likes
Answer
The figure of the buoy made by surmounting a right cone on a hemisphere is shown below:
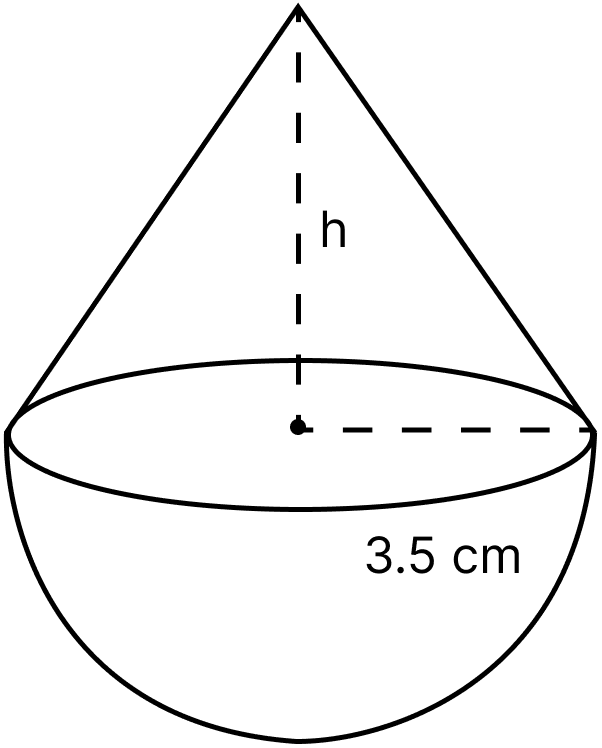
Radius of base of hemisphere = Radius of cone = 3.5 m.
Volume of hemisphere (V) =
Putting values,
Volume of cone = Volume of hemisphere.
∴ Volume of cone =
Volume of cone = .
Slant height of cone = l =
Putting values we get,
Surface area of the buoy = Curved Surface area of cone + Curved Surface area of hemisphere = πrl + 2πr2.
∴ Surface area of buoy =
Hence, the height of cone = 4.67 m and surface area of buoy is 141.17 m2.
Answered By
26 Likes
Related Questions
From a solid cylinder of height 30 cm and radius 7 cm, a conical cavity of height 24 cm and of base radius 7 cm is drilled out. Find the volume and the total surface of the remaining solid.
The adjoining figure shows a hemisphere of radius 5 cm surmounted by a right circular cone of base radius 5 cm. Find the volume of the solid if the height of the cone is 7 cm. Give your answer correct to two places of decimal.

A building is in the form of a cylinder surmounted by a hemisphere valted dome and contains of air. If the internal diameter of dome is equal to the total height of the building, find the height of the building.
A rocket is in the form of a right circular cylinder closed at the lower end and surmounted by a cone with the same radius as that of the cylinder. The diameter and the height of the cylinder are 6 cm and 12 cm respectively. If the slant height of the conical portion is 5 cm, find the total surface area and the volume of the rocket. (Use π = 3.14).