From a solid cylinder of height 30 cm and radius 7 cm, a conical cavity of height 24 cm and of base radius 7 cm is drilled out. Find the volume and the total surface of the remaining solid.

The figure is shown below:

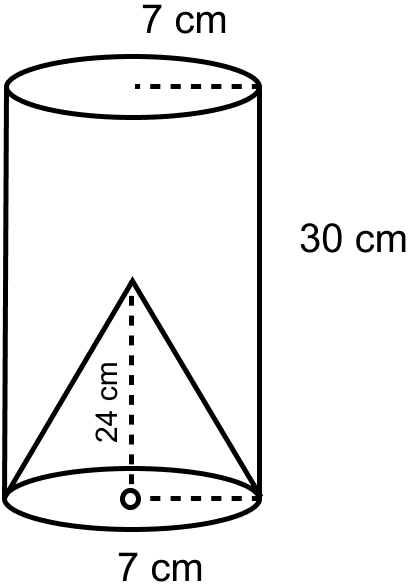
Radius of the solid cylinder = Radius of cone = r = 7 cm.

Height of the cylinder, H = 30 cm

Height of cone, h = 24 cm.

Slant height of cone, l = $\sqrt{h^2 + r^2}$.

Putting values we get,

l = $\sqrt{24^2 + 7^2} = \sqrt{576 + 49} = \sqrt{625} = 25$ m.

Volume of the remaining solid (V) = Volume of the cylinder - Volume of the cone.

$\therefore V = πr^2H - \dfrac{1}{3}πr^2h \\[1em] = πr^2(H - \dfrac{h}{3}) \\[1em] = \dfrac{22}{7} \times 7^2 \times (30 - \dfrac{24}{3}) \\[1em] = \dfrac{22}{7} \times 7^2 \times (30 - 8) \\[1em] = 22 \times 7 \times 22 \\[1em] = 3388 \text{ cm}^3.$

Total surface area of the remaining solid (S) = Curved surface area of cylinder + Area of base of cylinder + Curved surface area of cone.

$\therefore S = 2πrH + πr^2 + πrl \\[1em] = πr(2H + r + l) \\[1em] = \dfrac{22}{7} \times 7 \times (2 \times 30 + 7 + 25) \\[1em] = 22 \times (60 + 32) \\[1em] = 22 \times 92 \\[1em] = 2024 \text{ cm}^2.$

Hence, the volume of the remaining solid = 3388 cm³ and surface area = 2024 cm².