Mathematics
A circus tent is in the shape of a cylinder surmounted by a cone. The diameter of the cylindrical portion is 24 m and its height is 11 m. If the vertex of the cone is 16 m above the ground, find the area of the canvas used to make the tent.
Mensuration
90 Likes
Answer
The figure of the circus tent is shown below:
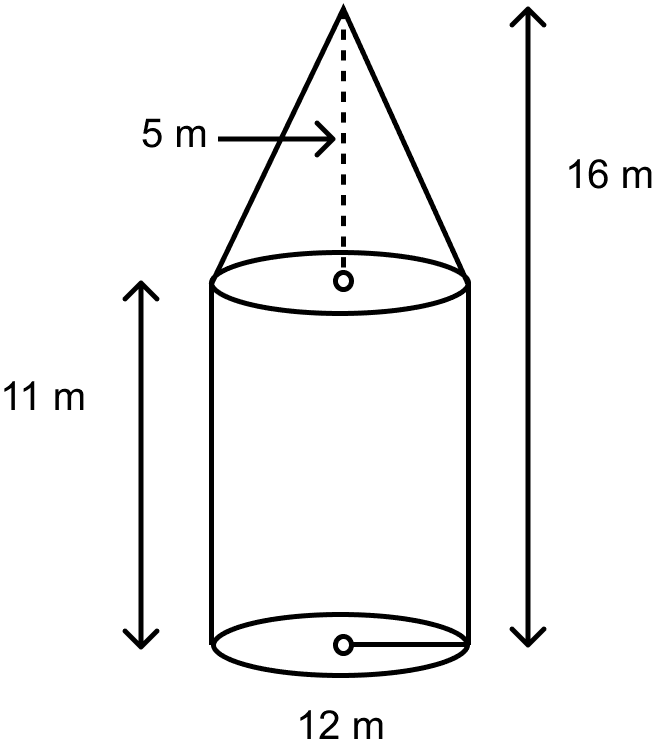
Diameter of cylindrical portion = 24 m
Radius of cylindrical portion (r) =
= = 12 m.
Height of the cylindrical part, H = 11 m.
Since vertex of cone is 16 m above the ground, height of cone, h = 16 - 11 = 5 m.
h = 5 m.
Radius of cone = 12 m.
∴ Radius of cone is also equal to r.
Slant height of the cone, l = .
l = m.
Area of canvas used to make the tent = Curved surface area of the cylindrical part + Curved surface area of the cone.
Area of the canvas used to make the tent = 2πrH + πrl = πr(2H + l).
Putting values we get,
Area of the canvas =
Hence, the area of the canvas used to make the tent is 1320 m2.
Answered By
34 Likes
Related Questions
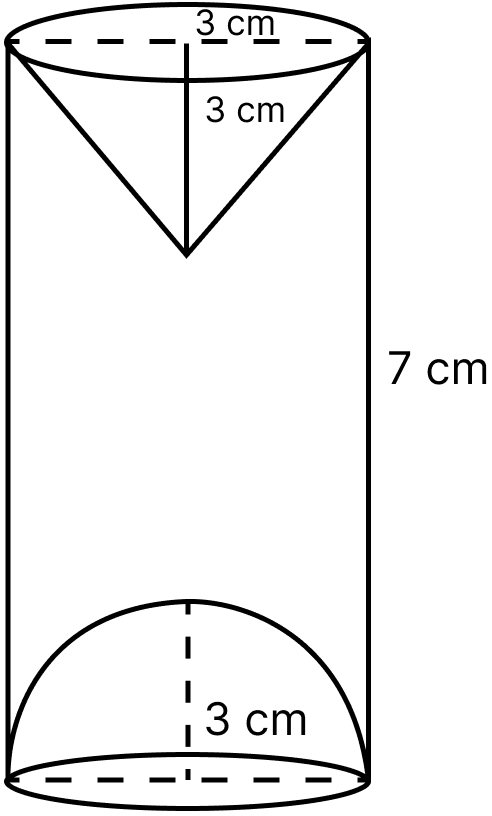
A hemispherical and conical hole are scooped out of a solid wooden cylinder. Find the volume of the remaining solid where the measurements are as follows :
The height of the cylinder is 7 cm, radius of each hemisphere, cone and cylinder is 3 cm. Height of cone is 3 cm. Give your answer correct to nearest whole number. Take π =
A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. If the total height of the toy is 15.5 cm, find the total surface area of the toy.
An exhibition tent is in the form of a cylinder surmounted by a cone. The height of the tent above the ground is 85 m and the height of the cylindrical part is 50 m. If the diameter of the base is 168 m, find the quantity of canvas required to make the tent. Allow 20% extra for folds and stitching. Give your answers to the nearest m2.
From a solid cylinder of height 30 cm and radius 7 cm, a conical cavity of height 24 cm and of base radius 7 cm is drilled out. Find the volume and the total surface of the remaining solid.