Mathematics
A toy is in the form of a cone of radius 3.5 cm mounted on a hemisphere of same radius. If the total height of the toy is 15.5 cm, find the total surface area of the toy.
Mensuration
43 Likes
Answer
The figure of the toy in the form of a cone surmounted on a hemisphere of same radius is shown below:

Total height of the toy = 15.5 cm
Radius of the base of the conical part (r) = 3.5 cm.
Height of the cone = 15.5 - 3.5 = 12 cm.
Slant height of the cone = l.
l =
Total surface area of the toy (T) = Curved surface area of cone + Curved surface area of hemisphere.
Hence, the total surface area of the toy is 214.5 cm2.
Answered By
28 Likes
Related Questions
A wooden article was made by scooping out a hemisphere from each end of a solid cylinder (as shown in the adjoining figure). If the height of the cylinder is 10 cm and its base is of radius 3.5 cm, find the total surface area of the article.

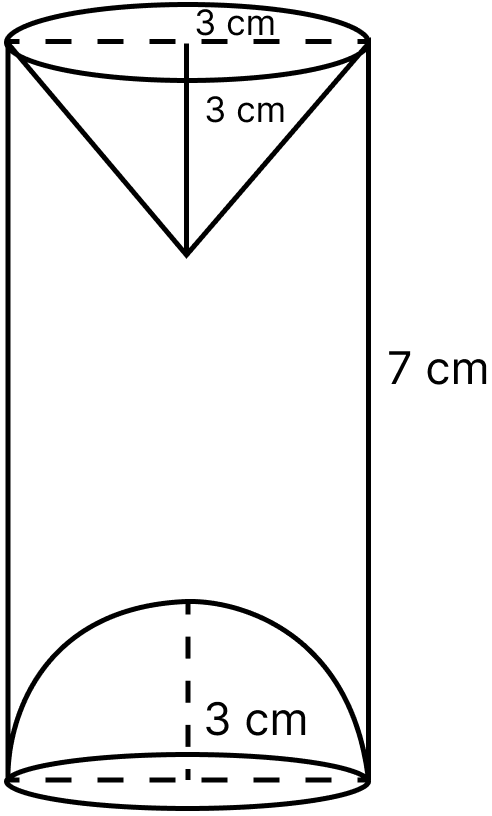
A hemispherical and conical hole are scooped out of a solid wooden cylinder. Find the volume of the remaining solid where the measurements are as follows :
The height of the cylinder is 7 cm, radius of each hemisphere, cone and cylinder is 3 cm. Height of cone is 3 cm. Give your answer correct to nearest whole number. Take π =
A circus tent is in the shape of a cylinder surmounted by a cone. The diameter of the cylindrical portion is 24 m and its height is 11 m. If the vertex of the cone is 16 m above the ground, find the area of the canvas used to make the tent.
An exhibition tent is in the form of a cylinder surmounted by a cone. The height of the tent above the ground is 85 m and the height of the cylindrical part is 50 m. If the diameter of the base is 168 m, find the quantity of canvas required to make the tent. Allow 20% extra for folds and stitching. Give your answers to the nearest m2.