Mathematics
A chord of length 48 cm is at a distance of 10 cm from the centre of a circle. If another chord of length 20 cm is drawn in the same circle, find its distance from the center of the circle.
Circles
16 Likes
Answer
From figure,
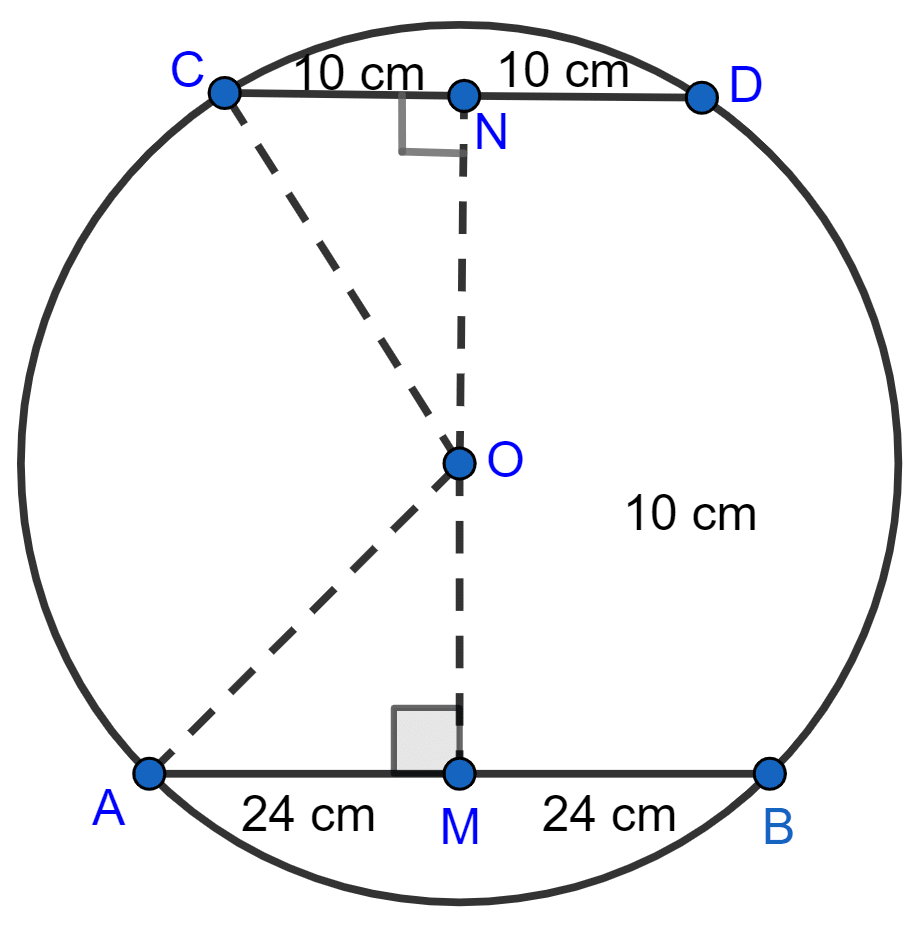
Since, OM ⊥ AB, it bisects it. (As perpendicular from center to chord bisects it)
∴ AM = MB = = 24 cm.
In right △AOM,
⇒ AO2 = OM2 + AM2 (By pythagoras theorem)
⇒ AO2 = 102 + 242
⇒ AO2 = 100 + 576
⇒ AO2 = 676
⇒ AO = = 26 cm.
Radius = 26 cm.
Since, ON ⊥ CD, it bisects it. (As perpendicular from center to chord bisects it)
∴ CN = ND = = 10 cm.
In right △CNO,
⇒ OC2 = ON2 + NC2 (By pythagoras theorem)
⇒ 262 = ON2 + 102
⇒ ON2 = 676 - 100
⇒ ON2 = 576
⇒ ON = = 24 cm.
Hence, the chord of length 20 cm is at a distance of 24 cm from the centre.
Answered By
10 Likes
Related Questions
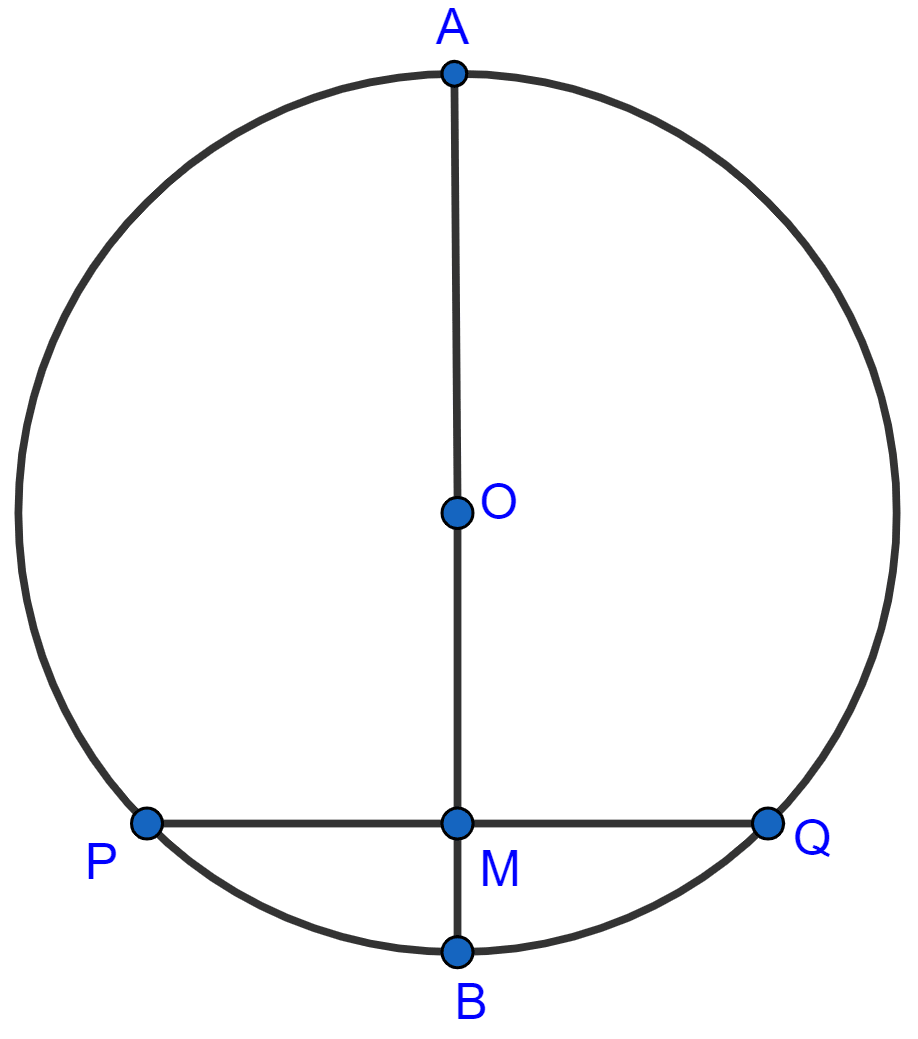
In the adjoining figure, a chord PQ of a circle with center O and radius 15 cm is bisected at M by a diameter AB. If OM = 9 cm, find the lengths of :
(i) PQ
(ii) AP
(iii) BP.
The radii of two concentric circles are 17 cm and 10 cm; a line PQRS cuts the larger circle at P and S and the smaller circle at Q and R. If QR = 12 cm, calculate PQ.
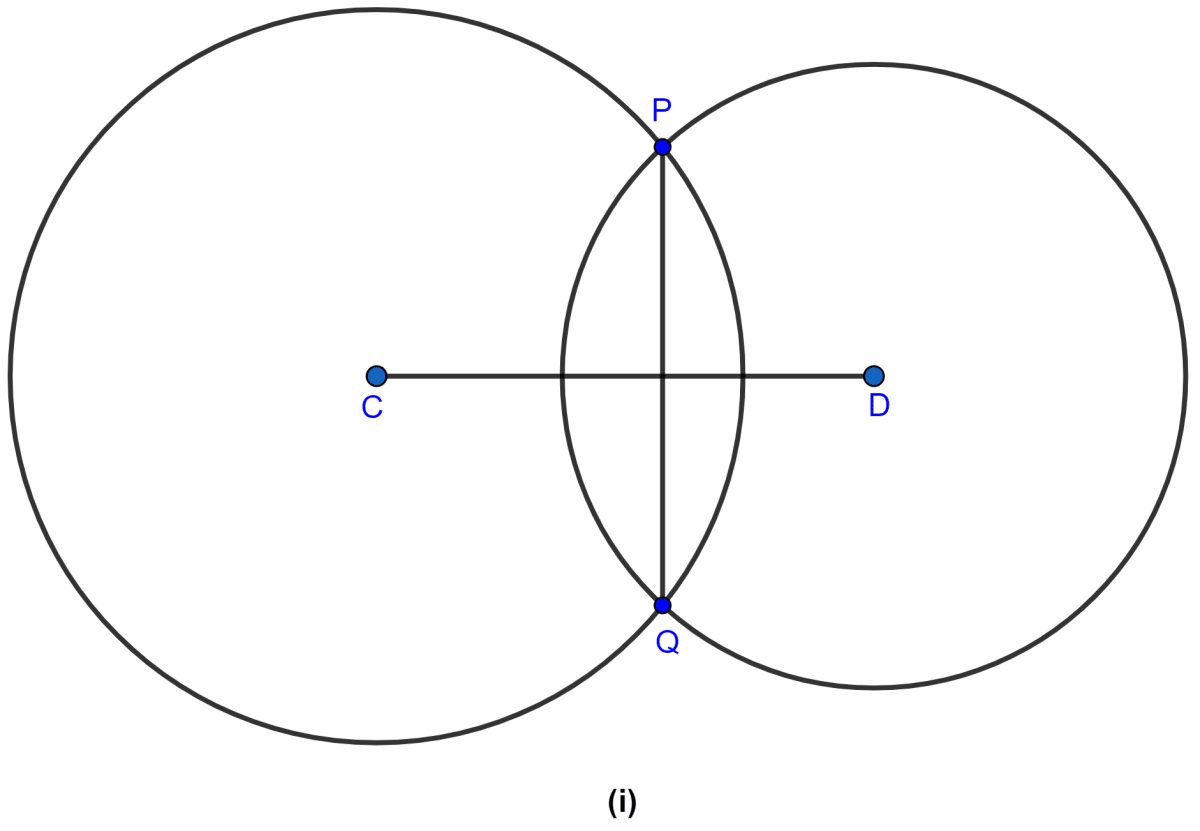
In the figure (i) given below, two circles with centers C, D intersect in points P, Q. If length of common chord is 6 cm and CP = 5 cm, DP = 4 cm, calculate the distance CD correct to two decimal places.
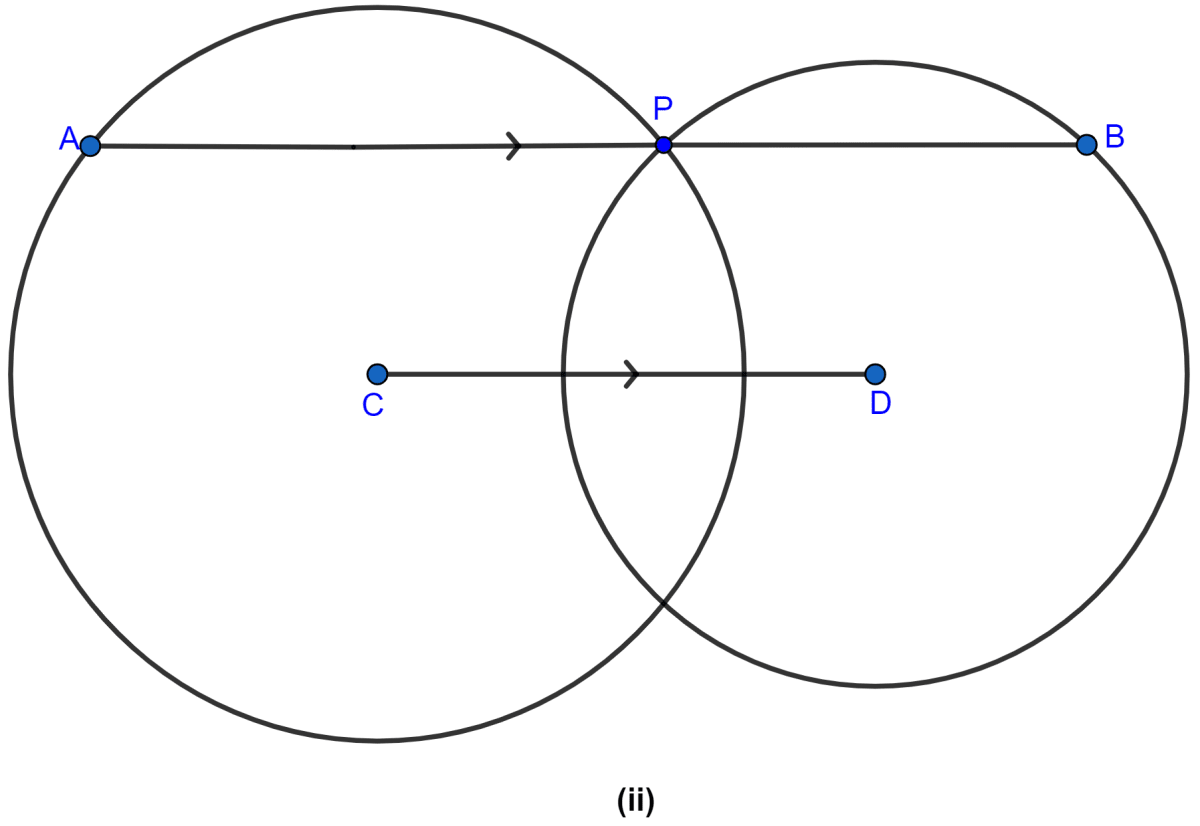
In the figure (ii) given below, P is a point of intersection of two circles with centers C and D. If the st. line APB is parallel to CD, prove that AB = 2CD.